라인 스위핑 알고리즘이란, 1차원 좌표(수직선)에 그려진 여러 선분을 합치는 알고리즘이다.

위의 그림과 같이, 수직선에 5개의 선분을 긋고자 한다고 해보자.
위의 그림에선, 여러 선분들이 서로 겹치지 않게 그려있지만 수직선은 1차원 좌표이기 때문에 실제로 수직선에 선분을 긋게 되면 선분들은 서로 겹치게 된다.

이런 식으로, 실제로 좌표에 선분을 긋게되면 범위가 겹치는 선분은 모두 하나로 합쳐지게 된다.
이런 식으로 여러 구간이 주어졌을 때, 겹치는 구간을 모두 합치고자 할 때 사용하는 알고리즘이 라인 스위핑 알고리즘이다.
위와 같은 선분에 대해서만 사용할 수 있는 것이 아니라, 시간처럼 시작과 끝이 주어질 수 있는 대상에 대해서는 모두 사용이 가능하다.
라인 스위핑
위처럼, 여러 구간을 하나로 합치려면 일반적으로는 이중 반복문으로 구현하게 된다.
현재 선분과 다른 모든 선분을 비교하여, 구간이 겹치는 선분이 있다면 하나로 합치는 것이다.
이런 방식은, O(N^2)의 시간복잡도를 지니게 된다.
너무 시간복잡도가 크기때문에, 이를 줄이기 위해 라인 스위핑을 사용하는 것이다.
라인 스위핑은 먼저 선분을 시작지점을 기준으로 정렬해야 한다.
입력이 아래와 같이 주어졌다고 해보자.

자료구조에 선분의 정보를 저장한 뒤, 시작점을 기준으로 정렬하게 되면
노란색 -> 초록색 -> 보라색 -> 하늘색 -> 갈색 순서로 선분을 처리하게 된다. (노란색과 초록색은 바뀔 수도 있다.)
먼저, 합쳐진 선분에 대한 정보를 MergeLine 이라는 곳에 저장한다고 해보자.
가장 처음 비교할 선분은 노란색 선분이다. 노란색 선분에 대해서는 비교할 정보가 없기 때문에 MergeLine을 최초에는 노란색 선분으로 저장해주어야 한다.

이후, MergeLine과 초록색 선분을 비교해보자.
MergeLine의 시작점 : 0
MergeLine의 끝점 : 2
초록색 선분의 시작점 : 0
초록색 선분의 끝점 : 7
이 떄, 시작점과 끝점을 모두 비교할 필요는 없다.
초록색 선분의 시작지점이 MergeLine의 끝점보다 작거나 같다면, 두 선분은 합칠 수 있는 것이라고 생각할 수 있다.
만약, 초록색 선분의 시작지점이 MergeLine의 끝점보다 크다면 두 선분은 합칠 수 없다고 생각할 수 있다.
현재, 두 선분의 관계를 보면, MergeLine의 끝점(2)보다 초록색 선분의 시작점(0)이 더 작기때문에, 두 선분은 합칠 수 있다.

위와 같이, MergeLine의 정보가 갱신되었다.
다음은 MergeLine과 보라색선분을 비교해보자.
위와 동일하게 계산해보면 보라색선분도 MergeLine과 합칠 수 있다.
두 선분을 합쳐도 MergeLine에 변화는 없다.
다음으로, MergeLine과 하늘색 선분을 비교해보자.
이번엔, 합칠 수 없다.
하늘색선분의 시작지점(8)이 MergeLine의 끝지점(7)보다 크기 때문이다.
그러므로 새로운 MergeLine을 하나 더 만들어야 한다.

이렇게, 하늘색 선분의 길이와 동일한 MergeLine를 하나 더 생성하였다.
이제는 새로 만들어진 이 MergeLine을 기준으로 비교를 진행할 것이다.
다음으로 비교할 선분은 갈색 선분이다.
갈색 선분은 MergeLine과 합칠 수 있으므로, 두 선분을 합쳐주면 모든 선분을 합치는 작업이 끝나게 된다.
코드 구현
먼저, 위 그림과 같이 5개의 선분을 입력받는다고 가정해보자.
//입력
int NumOfLines = 5;
std::vector<std::pair<int, int>> Lines;
Lines.resize(NumOfLines);
Lines[0] = { 0, 2 };
Lines[1] = { 8, 15 };
Lines[2] = { 3, 6 };
Lines[3] = { 0, 7 };
Lines[4] = { 13, 15 };
시작점과 끝점을 효율적으로 관리하기 위해, std::pair를 사용하였다.
선분은 정렬되지 않은 상태로 입력받았다.
먼저, 위에서 말했듯이 정렬을 해주어야 한다.
std::sort(Lines.begin(), Lines.end());
std::pair의 경우 정렬기준은 first가 우선이고, first가 같다면 second를 기준으로 정렬하게 된다.
그러므로 시작점(first)를 기준으로 정렬하는 현재 상황에선 정렬 함수를 직접 정의할 필요는 없다.
std::pair<int, int> MergeLine = Lines[0];
std::pair<int, int> CurLine = { 0, 0 };비교를 진행하기 위해, 이렇게 2개의 변수를 선언하였다.
MergeLine은 합쳐진 선분을 의미한다. 이 선분의 초기값은 가장 앞에있는 선분으로 잡아주었다.
CurLine은 현재 비교하고자 하는 선분이다. 초기값은 크게 의미는 없다. 아무값으로나 초기화해주어도 상관없다.
std::vector<std::pair<int, int>> MergeLines;
MergeLines.reserve(5);MergeLines는 합쳐진 선분들을 저장할 vector이다.
MergeLines는 선분의 개수를 초과할 수 없기 때문에, 전체 선분의 개수와 동일하게 5로 reserve해주었다.
(입력받는 선분의 개수가 너무 많을 땐, 메모리적으로 낭비가 심할 수 있기 때문에 std::list를 사용하는 것도 좋다.)
for (int i = 1; i < NumOfLines; i++)
{
CurLine = Lines[i];
if (CurLine.first <= MergeLine.second)
{
MergeLine.second = std::max(CurLine.second, MergeLine.second);
}
else
{
MergeLines.push_back(MergeLine);
MergeLine = CurLine;
}
}
MergeLines.push_back(MergeLine);위는 선분을 비교하는 함수이다.
현재 선분을 CurLine에 저장해준 뒤, MergeLine과 비교하도록 했다.
위에서 말했듯, CurLine의 시작지점과 MergeLine의 끝지점만 확인하였다.
두 선분을 비교할 때, 시작지점은 무조건 MergeLine이 더 앞에있거나 같을 수 밖에 없다.
(정렬된 상태로 merge를 진행했기 때문에)
그러므로, 두 선분을 합칠 때는 끝지점에 대해서만 갱신해주면 된다.
만약, MergeLine 이 (1, 2)이고, CurLine이 (1, 5)인 상황이 있을 수도 있다.
이 경우 CurLine과 MergeLine의 끝지점중 더 큰쪽으로 MergeLine을 갱신해야 하기 때문에
std::max를 사용하여 더 큰값을 저장해주었다.
만약, 두 선분이 겹치지 않는다면, 기존의 MergeLine은 벡터에 저장해주고 현재 선분으로 MergeLine을 갱신해주었다.
반복문이 다 끝나고 나서, 현재 MergeLine을 꼭 벡터에 다시 넣어주어야 한다.
마지막 MergeLine은 벡터에 저장되지 않았으니 말이다.
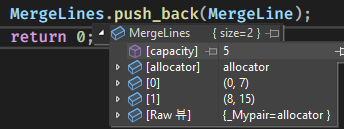
내부의 값을 보면, 위 사진과 같이 선분이 잘 합쳐져있는 것을 볼 수 있다.
코드 전문
#include <iostream>
#include <vector>
#include <algorithm>
int main()
{
int NumOfLines = 5;
std::vector<std::pair<int, int>> Lines;
Lines.resize(NumOfLines);
Lines[0] = { 0, 2 };
Lines[1] = { 8, 15 };
Lines[2] = { 3, 6 };
Lines[3] = { 0, 7 };
Lines[4] = { 13, 15 };
std::sort(Lines.begin(), Lines.end());
std::pair<int, int> MergeLine = Lines[0];
std::pair<int, int> CurLine = { 0, 0 };
std::vector<std::pair<int, int>> MergeLines;
MergeLines.reserve(5);
for (int i = 1; i < NumOfLines; i++)
{
CurLine = Lines[i];
if (CurLine.first <= MergeLine.second)
{
MergeLine.first = std::min(CurLine.first, MergeLine.first);
MergeLine.second = std::max(CurLine.second, MergeLine.second);
}
else
{
MergeLines.push_back(MergeLine);
MergeLine = CurLine;
}
}
MergeLines.push_back(MergeLine);
return 0;
}'C++ > 알고리즘' 카테고리의 다른 글
| 알고리즘 - 위상 정렬 (0) | 2024.06.01 |
|---|---|
| 알고리즘 - 단조 스택 (Monotonic Stack) (1) | 2024.04.26 |
| 알고리즘 - 펜윅 트리 (구간의 합 구하기) (0) | 2024.04.13 |
| 알고리즘 - 세그먼트 트리 (구간의 합 구하기) (0) | 2024.04.12 |
| 알고리즘 - 에라토스테네스의 체 (소수 판별) (0) | 2024.04.09 |