

집들이 이렇게 연결되어 있다고 가
정해보자.
저 모든 집들을 일단 두개의 마을로 분리해야 한다.

이런 식으로, 여러 집들을 두 개의 마을로 분할하는 것이다.
(물론, 두 개의 마을로 나누는 방법은 이 외에도 많다.)
이렇게, 두 마을을 분할했다면, 마을 사이의 도로를 제거하고, 각 마을의 도로를 최소화하여야 한다.

먼저, 마을 사이의 도로를 모두 제거하였다.
그런데, 보면 왼쪽 마을은 연결되어 있는 도로가 불필요하게 많다.

위의 그림과 같이, 도로를 하나 제거하여도, 모든 집이 연결되는 경우가 두 가지나 있기 때문이다.
두 경우 중에서, 도로 유지비의 합이 최소인 경우를 골라서, 그 때의 도로 유지비의 합을 반환하면 된다.
문제 풀이
이 문제는 최소 신장 트리(최소 스패닝 트리)를 이용하여 푸는 문제이다. 본인은 크루스칼 알고리즘을 활용하여 문제를 해결하였다.
크루스칼 알고리즘을 모른다면, 알고리즘을 공부하고 오도록 하자.
전체적으로 일반적인 크루스칼 알고리즘 문제와 똑같다. 하지만, 이 문제는 마을을 분리해야 한다는 조건이 하나 추가되었다. 그렇다면, 마을을 분리한 뒤에 도로를 제거하면 될까?
아니다. 도로를 제거하여 마을을 분리해도 된다.
무슨 말이냐면, 어쨋든 이 문제는 모든 집을 연결하면서, 간선의 가중치의 합의 최소를 구하는 문제이다.
그렇다면, 모든 집에 대해 일단 최소 신장 트리를 구성한 다음, 그중 가장 유지비가 비싼 간선 하나만 제거하여도, 두 개의 마을이 분리가 되는 것이다.
아래 그림을 보자.

이렇게, 집들이 도로로 연결되어 있다고 가정해보자.
이 집들에 대해 최소 신장 트리를 구성했을 때 아래와 같다. (임의로 가정한 최소 신장 트리이다.)

최소 신장 트리인 만큼 인접한 집과 집 사이엔, 하나의 간선만 연결되어 있다.
이 때, 하나의 간선을 제거하게 된다면, 해당 집과 집은 연결이 끊어지게 되고, 아래와 같아진다.
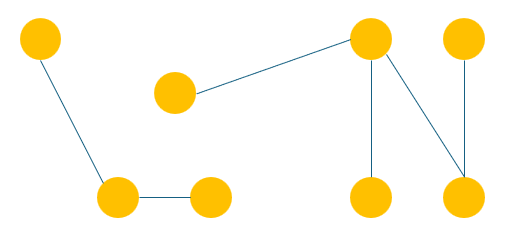
이렇게, 간선 하나만 제거하여도 두개의 마을로 분리되는 것이다.
그렇다면, 간선을 하나 제거할 때 가장 유지비가 비싼 간선을 제거한다면?
여러 집들을 두 마을로 분리하면서, 가중치의 합이 최소인 형태가 되는 것이다.
즉, 크루스칼 알고리즘을 이용해서 최소 신장 트리를 구성한다음, 가장 비싼 가중치의 간선만 제거하면 답을 구할 수 있다.
풀이 코드
int GetRootParent(int _Index)
{
if (Parents[_Index] == _Index)
{
return _Index;
}
Parents[_Index] = GetRootParent(Parents[_Index]);
return Parents[_Index];
}
void Setparent(int _Left, int _Right)
{
if (_Left < _Right)
{
Parents[GetRootParent(_Right)] = _Left;
}
else
{
Parents[GetRootParent(_Left)] = _Right;
}
}
bool isCycle(int _Left, int _Right)
{
int LeftRootParent = GetRootParent(_Left);
int RightRootParent = GetRootParent(_Right);
return (LeftRootParent == RightRootParent);
}
먼저, 크루스칼 알고리즘을 사용하기 위해 유니온 파인드 함수들을 정의하였다.
std::cin >> NumOfHouse >> NumOfRoad;
Parents.resize(NumOfHouse + 1);
for (int i = 1; i <= NumOfHouse; i++)
{
Parents[i] = i;
}
이후, 입력을 받았고, 부모 배열을 초기화 해주었다.
struct Link
{
int Start = 0;
int End = 0;
int Cost = 0;
};
bool compare(const Link& _Left, const Link& _Right)
{
return _Left.Cost < _Right.Cost;
}
std::vector<Link> Links(NumOfRoad);
for (int i = 0; i < NumOfRoad; i++)
{
std::cin >> Links[i].Start >> Links[i].End >> Links[i].Cost;
}
std::sort(Links.begin(), Links.end(), compare);
간선의 정보를 저장할 구조체를 선언하였고, 정렬하기 위한 compare함수를 정의하였다.
이후 간선의 정보를 입력받았으며, 해당 간선을 가중치 기준으로 정렬해주었다.
int SumCost = 0;
int LastWeight = 0;
for (int i = 0; i < NumOfRoad; i++)
{
if (isCycle(Links[i].Start, Links[i].End) == false)
{
SumCost += Links[i].Cost;
Setparent(Links[i].Start, Links[i].End);
LastWeight = Links[i].Cost;
}
SumCost -= LastWeight;
std::cout << SumCost;
이후, 일반적인 크루스칼 알고리즘과 동일하게 가중치의 합을 구해주었다.
그런데, 위에서 말했듯이 이렇게 연결한 다음, 가장 가중치가 비싼 간선을 제거해주어야 한다.
그러므로, 가장 마지막에 연결된 간선의 가중치를 LastWeight에 기록하였고, 마지막에 LastWeight를 가중치의 합에서 빼주었다.
(간선은 가중치 순으로 정렬되어 있기 때문에, 가장 마지막에 연결된 간선이 가중치가 가장 크다.)
SumCost를 출력해주면 문제는 끝이다.

코드 전문
#include <iostream>
#include <vector>
#include <algorithm>
void Init()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
}
struct Link
{
int Start = 0;
int End = 0;
int Cost = 0;
};
std::vector<int> Parents;
int NumOfHouse = 0;
int NumOfRoad = 0;
bool compare(const Link& _Left, const Link& _Right)
{
return _Left.Cost < _Right.Cost;
}
int GetRootParent(int _Index)
{
if (Parents[_Index] == _Index)
{
return _Index;
}
Parents[_Index] = GetRootParent(Parents[_Index]);
return Parents[_Index];
}
void Setparent(int _Left, int _Right)
{
if (_Left < _Right)
{
Parents[GetRootParent(_Right)] = _Left;
}
else
{
Parents[GetRootParent(_Left)] = _Right;
}
}
bool isCycle(int _Left, int _Right)
{
int LeftRootParent = GetRootParent(_Left);
int RightRootParent = GetRootParent(_Right);
return (LeftRootParent == RightRootParent);
}
int main()
{
Init();
std::cin >> NumOfHouse >> NumOfRoad;
Parents.resize(NumOfHouse + 1);
for (int i = 1; i <= NumOfHouse; i++)
{
Parents[i] = i;
}
std::vector<Link> Links(NumOfRoad);
for (int i = 0; i < NumOfRoad; i++)
{
std::cin >> Links[i].Start >> Links[i].End >> Links[i].Cost;
}
std::sort(Links.begin(), Links.end(), compare);
int SumCost = 0;
int LastWeight = 0;
for (int i = 0; i < NumOfRoad; i++)
{
if (isCycle(Links[i].Start, Links[i].End) == false)
{
SumCost += Links[i].Cost;
Setparent(Links[i].Start, Links[i].End);
LastWeight = Links[i].Cost;
}
}
SumCost -= LastWeight;
std::cout << SumCost;
return 0;
}
'코딩테스트 문제 풀이 (C++)' 카테고리의 다른 글
| 백준 1987 - 알파벳 (C++) (1) | 2024.04.19 |
|---|---|
| 백준 1107 - 리모컨 (C++) (0) | 2024.04.19 |
| 백준 9663 - N_Queen (C++) (0) | 2024.04.16 |
| 백준 16563 - 어려운 소인수분해 (C++) (0) | 2024.04.16 |
| 프로그래머스 - 땅따먹기 (C++) (0) | 2024.04.16 |