

위와 같은 그림이 있다고 쳐보자. 우리는 가장 위의 행부터 한칸씩 아래로 내려와야 한다.
내려올 때, 같은 열은 밟고 내려올 수 없다.
위의 그림에서 화살표를 보면, 1이 적혀있는 1행 1열에서 시작한다면, 2행에 있는 6, 7, 8 로는 이동할 수 있지만,
2행 1열인 5가 적힌 곳으로는 내려올 수 없다. ( 열이 같기 때문에 )
다시, 2행에 있는 8에서부터 이동한다고 해보자. 3행에 있는 4, 3, 2로는 이동할 수 있지만 1로는 이동할 수 없다.
이런 규칙을 지닌 채로, 밟은 발판의 값을 모두 더하면서 가장 마지막 행까지 이동하면 된다.
여러 경우의 수중 밟은 발판의 값의 총 합의 최대값을 구하면 된다.
1->6->4의 경로로 이동했다면, 밟은 발판의 총 합은 11이 될것이고
2->5->3의 경로로 이동했다면, 밟은 발판의 총 합은 10이 될것이다.
위의 그림에서는 5->7->4의 경로로 이동하여 나온 16이라는 값이 밟은 발판의 총 합의 최대치이다.
문제풀이
이 문제는 전형적인 DP문제이다.
먼저, 현재 발판까지 이동하면서 구한 발판의 값의 총 합을 M이라고 해보자.

위의 그림을 보자.
2행에 있는 빨간색 5의 M이 최대값이 되려면, 당연히 이전 행에서 밟은 발판이 최대값이 되어야 한다.
그렇기 때문에, 보라색 5를 밟고 빨간색 5로 이동하는 것이 5의 입장에선 M이 최대가 되는 경로이다.

빨간색 8의 입장에서도 보자. 이전 행에서 값이 가장 큰 발판은 5이지만, 같은 열이기 떄문에 5->8의 경로는 불가능하다. 그렇기 때문에 5를 제외한 나머지 값중 최대값인 3번 발판을 밟고 8로 이동하게 되면 8번 발판에서 M은 최대가 된다.
이렇게, 2행에 있는 발판의 값을 각 발판에서 M의 최대값으로 갱신해보겠다.
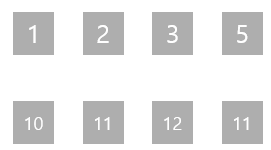
각 발판의 값은 이렇게 갱신할 수 있다.
이렇게 값을 갱신해준 이유는 각 발판을 밟고 지나갈 수 있는 경로중 최대값에 대해서만 계산하면 되기 때문이다.

값을 갱신하지 않은 위의 상태라고 해보자.
3행 1열에서 M의 최대값을 구하기 위해, 2행 2열을 거쳐오는 경우중 M의 최대값, 2행 3열을 거쳐오는 경우중 M의 최대값, 2행 4열을 거쳐오는 경우중 M의 최대값을 구해야한다.
지금은 문제가 3행밖에 없어서 복잡해보이지 않지만 만약 50행까지 있다고 가정해보면?
50행 1열에서 M의 최대값을 구하려면,49행 2열의 M의 최대값, 49행 3열의 M의 최대값, 49행 3열의 M의 최대값을 구해야하고, 49행 2열의 M의 최대값은 48행 1열의 M의 최대값, 48행 3열의 M의 최대값........... 쭉 이렇게 계속 계산해야 한다.
50행이라면 계산해야 하는 경우의 수가 3^49승이 될 것이다.
하지만, 위에서 미리 값을 갱신하면서 내려오게 되면, 이전 행에서 M의 최대값을 구하기 위한 연산을 중복해서 할 필요가 없어지기 때문에, 이전 행의 3개 열만 확인하면 된다.
i행 j열의 최대값 M을 구하는 경우의 수가 3^(i-1) 에서 3으로 줄어들게 된 것이다.
이제, 값을 갱신한 상태로 답을 구해보자.

이렇게 값을 갱신항 상태로, 다음 행의 최대값을 구해보자.
위의 행에 있는 4개의 열중 본인의 열과 같은 값을 제외하고 나머지 중에서 가장 큰 값을 찾아서 본인의 값과 더하면 된다.

최종적으로 위와 같은 모습으로 값의 갱신이 종료되었다.
아래 4개의 열이 가진 값중 최대값인 16을 답으로 반환하면 끝난다.
아래와 같이 주어진 입력에 대해서 한 번 더 테스트해보자.

이러한 과정을 거칠 것이고, 결과적으로 답은 가장 마지막 행의 최대값인 23이 될 것이다.
코드 풀이
int Height = land.size();
std::vector<std::vector<int>> DP(Height, std::vector<int>(4, 0));
먼저, 입력으로 주어진 2차원 배열의 크기를 이용해서 높이를 구해준 뒤, 입력의 사이즈와 동일한 DP배열을 만들어주었다.
DP[0][0] = land[0][0];
DP[0][1] = land[0][1];
DP[0][2] = land[0][2];
DP[0][3] = land[0][3];
이후, DP배열의 1행 값을 초기화해주었다.
왜냐하면, 이 문제에선 이전 행의 값을 기준으로 DP배열을 갱신할 것인데 1행은 이전의 행이 없기 때문에 입력된 값을 그대로 넣어준 것이다.
for (int i = 1; i < Height; i++)
{
for (int j = 0; j < 4; j++)
{
int Max = 0;
for (int k = 0; k < 4; k++)
{
if (j == k)
{
continue;
}
if (Max < DP[i - 1][k])
{
Max = DP[i - 1][k];
}
}
DP[i][j] = Max + land[i][j];
}
}
위의 코드는 DP배열을 갱신하는 코드이다.
가장 바깥 반복문에서는 행의 크기만큼 반복문을 돌아주고 있다.
1행부터 가장 마지막 행까지 DP배열을 갱신하는 것이다.
내부에는 2중반복문이 존재한다.
먼저,(i, j)에서 발판 값의 총 합의 최대값을 구하려면, (i-1)행에 있는 4개의 발판을 검사해야 한다.
그 중 최대값을 가져와서 i행 j열의 DP배열에 대입해주었다.
이 과정을 i행에 있는 4개의 발판에 대해 모두 반복해주었다.
이 반복문이 끝나면, DP배열은 모두 각 발판에 도달하는 경우중 M의 최대값으로 갱신되어 있을 것이다.
return *std::max_element(DP[Height - 1].begin(), DP[Height - 1].end());
답으로는 마지막 행에서 최대값을 반환해주면 끝이다.
아래는 코드 전문이다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int solution(vector<vector<int>> land)
{
int Height = land.size();
std::vector<std::vector<int>> DP(Height, std::vector<int>(4, 0));
DP[0][0] = land[0][0];
DP[0][1] = land[0][1];
DP[0][2] = land[0][2];
DP[0][3] = land[0][3];
for (int i = 1; i < Height; i++)
{
for (int j = 0; j < 4; j++)
{
int Max = 0;
for (int k = 0; k < 4; k++)
{
if (j == k)
{
continue;
}
if (Max < DP[i - 1][k])
{
Max = DP[i - 1][k];
}
}
DP[i][j] = Max + land[i][j];
}
}
return *std::max_element(DP[Height - 1].begin(), DP[Height - 1].end());
}

'코딩테스트 문제 풀이 (C++)' 카테고리의 다른 글
| 백준 9663 - N_Queen (C++) (0) | 2024.04.16 |
|---|---|
| 백준 16563 - 어려운 소인수분해 (C++) (0) | 2024.04.16 |
| 백준 14500 - 테트로미노 (C++) (0) | 2024.04.13 |
| 백준 9020 - 골드바흐의 추측 (C++) (0) | 2024.04.09 |
| 프로그래머스 - 점 찍기 (C++) (0) | 2024.04.08 |