에라토스테네스의 체란, 일정 범위안에 있는 숫자들 중 소수만와 소수가 아닌 수를 구별하기 위한 알고리즘이다.

이렇게, 1부터 25까지의 숫자가 있다고 해보자.

이중에 소수만을 판별하면, 이렇게 된다.
이 그림처럼 소수만 걸러내는 알고리즘이 에라토스 테네스의 체이다.
그렇다면, 어떻게 알고리즘이 작동할까?
어렵지 않다.
먼저 소수란, 1과 본인을 제외한 어떠한 약수도 가지지 않는 수이다.
다르게 말하면, 1이 아닌 다른 어떠한 수의 배수도 되지 않는다는 뜻이다.
그렇다면, 2부터 시작해서 25까지 배수를 모두 제거한다면 남는 수가 소수라고 할 수 있지 않을까?
그림으로 보자.

이게 최초의 상태이다.
여기서 2의 배수를 먼저 제거해보자.
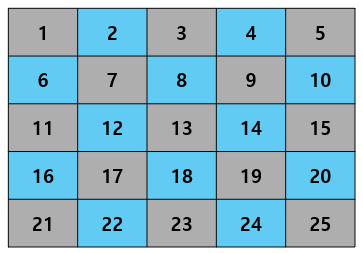
파란색으로 칠해진 부분이 제거된 숫자이다.
2의 배수를 모두 제거해보았으니, 3의 배수도 제거해보도록 하겠다.

이번엔 5의 배수도 지워보자.

이렇게 되었다. 5까지밖에 반복문을 돌지 않았는데도 소수만 남은 상태가 되었다.
그런데 보면 한 가지 문제점이 보인다.
2, 3, 5 또한 소수인데 불구하고 함께 제거해버린 것이다.
이런 일을 방지하기 위해, 배수를 제거할 때엔 본인은 제외하고 다음 배수부터 제거하는 것이 옳다.
2, 3,5 를 다시 추가해주면 아래와 같이 소수만 남는 것을 볼 수 있다.

마지막으로, 1의 경우는 소수가 아니다.
2의 배수부터 제거했기 때문에 마지막에 1이 남아있는 것을 볼 수 있다.
그러므로 1도 제거해주자.

이렇게 배수를 차례대로 지워나가면서 소수만 걸러내는 것이 에라토스 테네스의 체이다.
매우 간단하다.
하지만, 상식적으로 생각했을 떈 1~25까지 반복문을 다 돌아야할 것 같은데
실제로는 2~5까지만 돌았음에도 모든 소수가 제거되었다.
왜 그럴까?
이는 우연이 아니다. 실제로 1~N까지의 소수를 판별하고 싶다면, sqrt(N) 까지의 배수만 검사해도 모든 소수를 판별할 수 있다.
다음은 이에 대한 수학적 증명이다. 어렵진 않으니 참고하도록 하자.
먼저, N이라는 자연수는 어떠한 실수의 제곱으로 표현할 수 있다.
N = m * m; 이라고 표현해보자.
이번엔 N을 어떠한 두 약수의 곱으로 표현해보자.
N = a * b 가 될 것이다.
여기서 a,b 와 m의 관계를 생각해보자.
먼저 a * b = m * m 이다.
이 식을 보면 3가지의 경우를 나누어 볼 수 있다.
1. a == m , b == m 인 경우
당연히 a와 b가 m과 동일한 경우가 있을 것이다.
2. a > m, b > m 인 경우
다음 경우를 생각해보면, a와 b가 모두 m보다 클 수는 없다.
m보다 큰 두 수의 곱이라면 당연히 N보다 큰 값이 나오기 때문이다.
그러므로, 이러한 경우는 존재하지 않는다.
3. a < m , b > m 혹은 a >m , b < m 인 경우
a과 b가 m과 같지 않은 수라고 한다면, 두 숫자중 하나는 반드시 m보다 커야하고 남은 하나는 m보다 작아야 한다.
둘 다 m보다 크다면 a와 b의 곱은 N보다 큰 값이 나올 것이며, 둘 다 m보다 작다면 a와 b의 곱은 N보다 작은 값이 나올 것이다.
즉, N이라는 숫자는 반드시 sqrt(N)보다 작거나 같은 수의 배수가 될 것이다.
그러므로, 1~sqrt(N)까지의 수의 배수만 검사하여도 1~N 까지의 모든 배수를 제거할 수 있는 것이다.
코드 구현
이를 코드로 구현해보자.
int N = 100;
std::vector<int> Nums(N + 1, -1);먼저, N을 100이라고 가정해보자.
Nums 배열의 값은 최초에 -1로 초기화 하였다.
만약, 해당 인덱스가 소수가 아니라고 판별된다면 값을 0으로 바꿀 것이다.
당연히 int가 아닌 bool값을 활용하여 구현하여도 된다.
Nums[1] = 0;
1은 소수가 아니므로, 먼저 제거해주자.
for (int i = 2; i * i <= N; i++)
{
if (Nums[i] != -1)
{
continue;
}
for (int j = i + i; j <= N; j += i)
{
Nums[j] = 0;
}
}
그 다음은 위와 같이 반복문을 돌리면 된다.
반복문의 조건을 보면, i * i <= N 까지로 조건을 설정해두었다.
위에서 말했듯이 N의 제곱근까지만 반복문을 돌면 된다.
i * i <= N 이나 i <= sqrt(N) 이나 동일하기 때문에 편한대로 사용하면 된다.
i*i는 매 프레임마다 곱하기 연산을 해주어야 하지만, sqrt(N)의 경우 처음 한 번만 하고 변수에 저장한 뒤 사용하면 되기 때문에 최적화를 조금이라도 노리려면 sqrt(N)을 하는게 더 좋을 수도 있다.
(다만 sqrt연산 자체가 곱하기에 비해 매우 느린 편이라 N이 충분히 크지 않다면 별 효과 없을 수도 있다.)
이후 내부 코드를 보자.
해당 인덱스의 값이 이미 0이라면, 이미 제거된 수이다.
당연히 이 숫자의 배수도 제거되었을테니 검사할 필요 없이 continue하면 된다.
제거되지 않은 수라면 그 숫자의 배수를 모두 지워나가면 된다.
위에서 말했듯이, 시작 인덱스는 i부터가 아니라, i + i 부터 시작하고 있다.
첫 번째 수는 반드시 소수이기 때문에 두 번째 배수부터 제거해나가면 된다.
이러면 에라토스 테네스의 체 끝이다.
이제, 배열의 값을 기반으로 남은 소수를 출력해보면 아래와 같이 소수만 걸러져 나오는 것을 확인할 수 있다.

에라토스 테네스의 체는 어렵지 않은 알고리즘이다.
하지만, 소수에 관한 문제가 나온다면 거의 100%확률로 사용되는 알고리즘이기도 하다.
알고 있는 것과 모르는 것은 문제를 푸는 것에 있어 천지차이이기 때문에 반드시 숙지하도록 하자.
'C++ > 알고리즘' 카테고리의 다른 글
| 알고리즘 - 펜윅 트리 (구간의 합 구하기) (0) | 2024.04.13 |
|---|---|
| 알고리즘 - 세그먼트 트리 (구간의 합 구하기) (0) | 2024.04.12 |
| 알고리즘 - 유니온 파인드 (노드의 집합 판별하기) (0) | 2024.04.09 |
| 알고리즘 - 유클리드 호제법 (두 수의 최대 공약수 구하기) (0) | 2024.04.08 |
| 알고리즘 - CCW (세 점의 방향 판별하기) (0) | 2024.04.07 |