유니온 파인드란, 노드간의 집합을 구분하는 알고리즘이다.

위 그림과 같이 10개의 노드가 있다고 해보자.
이 때, 같은 색을 가진 노드끼리 구분하여 집합을 연결하고 싶다.

이런 식으로 말이다.
그렇다면, 어떻게 이렇게 구분을 지을 수 있을까?
가장 간단한 방법은 배열을 만드는 것이다.
배열을 만들어서 파란색이면 1번, 초록색이면 2번, 주황색이면 3번으로 입력한 뒤,
배열을 1~N까지 순회하며 값을 갱신해주면 된다.
하지만, 다음의 경우엔 어떨까?
위 문제처럼 직접적으로 어떤 노드가 파란색인지 초록색인지 정보가 없고, 두 노드가 색이 같다는 정보만 주어지는 것이다.
예를 들어 입력이 아래처럼 들어왔다고 해보자.
1 2
2 3
3 4
5 6
5 7
8 10
9 10
12가 같은색이고, 23이 같은 색이고 34가 같은 색이다.
56이 같은 색이고 57이 같은 색이다.
8 10이 같은 색이고, 9 10이 같은 색이다.
이렇게, 어떤 노드가 같은 색을 가지고 있는 가에 대한 정보만 주어지고, 정확히 무슨 색인지 주어지지 않는다면
위에서처럼 배열을 순회하며 값을 특정 색상으로 갱신하는 방법은 불가능해진다.
이런 경우에 사용하는 알고리즘이 union_Find알고리즘이다.
union - find 알고리즘은 이름 그대로, Union과 Find의 2개의 기능으로 구성된다.
1. Union
: 같은 속성을 지닌 노드들을 하나의 집합으로 합치는 것.
2. Find
: 노드가 어느 집합에 속하는지 찾아보는 것.
그렇다면 그걸 어떻게 구현하게 될까?
아래 그림을 보자.

정확한 색은 알 수 없지만, 위와 같은 연결 관계가 주어져있다는 것은 입력을 통해 확인하였다.
그렇다면, 연결된 노드끼리 합쳐서 하나의 집합으로 만들어 볼 수 있을 것이다.
이 과정을 union이라고 한다.

위에서 그림을 보면, 12, 34, 23의 연결관계를 보면 오른쪽처럼 1-2-3-4로 하나로 묶을 수 있다.
나머지 노드들도 위의 그림처럼 하나의 집합으로 묶을 수 있을 것이다.
그런데, 단순히 이렇게 집합만 묶어버리면 Find연산을 할 수가 없어진다.
Find연산이란, 특정 노드가 어느 집합에 속해있는가를 찾는 연산인데 이렇게 하나로 묶어버리기만 하면, 집합간의 관계를 구별할 수가 없다. 무슨 말이냐면, 1과 5가 같은 집합에 속해있는가? 3과 7이 같은 집합에 속해있는가? 를 묻는다면 그걸 구별할 방법이 없다는 것이다.
그렇기 때문에, 트리 구조를 사용할 것이다.

이렇게, 선형적인 연결에서 트리구조로 바꾸게 되면, 루트 노드의 인덱스를 통해 집합을 서로 구분할 수 있게 된다.
예를 들어보면, 2가 속한 집합의 루트노드는 1이고 3이 속한 집합의 루트노드 역시 1이다.
그러므로 두 노드는 같은 집합에 속한다고 표현할 수 있게 되는 것이다.
즉, Union이란 같은 속성을 지닌 노드를 트리구조로 구축하는 것이며
Find란 노드의 루트 노드를 검사하는 일이 되는 것이다.
그렇다면, 구체적으로 어떻게 Union과 Find가 작동하는지 알아보도록 하자.
유니온 파인드
먼저, 각 노드별로 부모 노드가 어디인가를 저장하는 배열을 하나 선언해야 한다.
std::vector<int> Parents;
노드의 개수가 10개라고 했을 때, 배열을 표로 그려보자.

각 배열의 원소는 인덱스에 해당하는 노드의 부모 노드가 누구인가를 가리키는 것이다.
예를 들어, 2번 원소의 부모노드가 6번이라고 한다면 2번 원소의 값은 6이 되는 것이다.
최초에는 이 배열의 값을 인덱스로 초기화 할 것이다.

이 값은 Union과정을 거치면서 계속 바뀌게 될 것이다. 하지만, 변하지 않고 계속 자기 자신을 가리키게 될 노드들도 있다. 그건 바로 루트노드이다.
루트 노드의 경우엔, 부모노드가 존재하지 않는다. 그렇기 때문에 이 배열에서 인덱스와 원소의 값이 동일하다면 그 노드는 루트 노드라고 가정할 것이다.
먼저, 입력은 아래와 같이 주어진다고 가정하도록 하겠다.
1 2
2 3
3 4
5 6
5 7
8 10
9 10
먼저 주어진 1, 2에 대해서 확인해보자.
현재 배열 내부에서는 모든 노드가 본인 자신을 부모 노드로 가리키고 있다.

1번과 2번도 이렇게 연결되지 않고 분리되어 있는 상태인 것이다.
하지만, 입력을 보면 1과 2는 연결되어 있다는 것을 확인할 수 있다.
그러므로 1과 2를 이어주어야 한다.

이려렇게 트리구조로 연결해주도록 하겠다.
(노드를 연결할 때, 인덱스가 더 작은 노드를 부모로 둘 것인가 더 큰 노드를 부모로 둘 것인가를 생각해야 하는데, 어느 방식으로 하든 결과는 동일하다. 하지만 하나의 기준을 선택했다면 모든 노드에 대해 동일한 기준을 적용해야 한다. 본인은 인덱스가 더 작은 노드를 부모 노드로 연결하도록 하였다.)
이렇게 연결하고 나니, 2번 노드의 부모 노드는 1번이 되었다.
그렇다면, 배열의 값을 갱신해야 한다.

이렇게 값을 갱신하였다.
이번엔, 두 번째 입력을 보자.

2와 3이 연결되어 있다고 한다.
그렇다면, 이건 아래 그림과 같이 연결해줄 수 있다.

이렇게 연결하면, 배열에서 3번째 원소의 값은 2가 될 것이다.
하지만, 이렇게 연결하게 되면 문제가 있다.
이렇게 연결하게 되면 3의 루트 노드를 찾기 위해 3->2->1 이렇게 선형으로 탐색해야 한다.
노드가 적을 땐 문제가 없을지 몰라도, 노드가 1억개정도 된다고 치면 1억번을 타고 올라가서 루트 노드를 구해야 하는 것이다. 이 과정이 굉장히 비효율적이다.
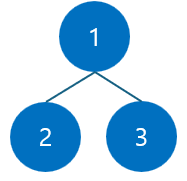
그렇기 때문에 위 그림과 같이 연결해줄 것이다.
이 알고리즘에서 중요한 것은 2 3 이라는 입력이 주어졌을 때, 2와 3이 직접적으로 연결된다는 것이 아니라 두 숫자가 같은 속성을 공유한다는 것이다.
즉, 연결 관계는 중요하지 않고 같은 집합에만 존재하면 된다는 것이다.
그러므로, 위와 같은 트리로 구현할 것이다.
배열에는 3이 속한 트리의 루트 노드를 저장해주도록 하겠다.

똑같은 과정으로 다른 노드에도 적용을 하게 되면 아래와 같이 트리를 구성할 수 있다.

또한, 배열의 값은 아래와 같을 것이다.

이제 집합이 완성되었으니, Union과정은 끝난 것이다.
하지만, 문제가 한가지 있다.
항상 위의 트리처럼 깊이가 2인 깔끔한 트리구조를 구현할 수 있다면 좋겠지만 그렇게 되지는 않는다.
2 3, 3 1의 입력을 받았다고 가정해보자.
먼저 2와 3을 연결해주면 아래 그림과 같을 것이다.
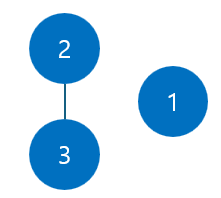
여기서 1을 연결해주면?

이런 형태의 트리가 되고 만다.
그런데 이는 위에서 말했던 것처럼 비효율적인 트리 형태이다.
즉 완벽하게 깊이가 2인 트리를 항상 유지하는 것은 아니라는 것이다.
이걸 최적화하는 기법도 있는 걸로 아는데, 그 부분은 본인도 조금 더 찾아봐야 할 듯 하다.
이제 이 알고리즘을 코드로 구현해보자.
코드 구현
std::vector<int> Parents;먼저, 부모 노드를 저장할 배열을 선언하였다.
입력은 아래와 같이 들어온다고 가정하도록 하겠다.
10
8
1 2
2 3
3 4
5 6
5 7
8 10
9 10
첫 번째 입력은 노드의 개수를 의미한다.
두 번째 입력은 이후에 주어질 집합 정보의 수를 의미한다.
다음은 집합 정보가 주어진다.
1 2 가 주어진다면, 1과 2는 같은 집합에 속한다는 의미이다.
입력을 저장해보자.
int NumOfNode = 0;
int NumOfLink = 0;
std::cin >> NumOfNode >> NumOfLink;
std::vector<std::pair<int, int>> Links(NumOfLink, {0, 0});
for(int i = 0; i < NumOfLink; i++)
{
std::cin >> NumOfLink[i].first;
std::cin >> NumOfLink[i].second;
}
입력은 이렇게 하면 끝이다.
이후, parents 배열의 값을 인덱스로 초기화해주었다.
Parents.resize(NumOfNode + 1);
for (int i = 0; i <= NumOfNode; i++)
{
Parents[i] = i;
}
이제, Root노드를 구하는 함수를 먼저 만들어보자.
int GetRootParents(int _Num)
{
if (Parents[_Num] == _Num)
{
return _Num;
}
else
{
return GetRootParents(Parents[_Num]);
}
}
먼저, 현재 배열의 값과 인덱스가 동일하다면 그 노드는 루트노드라고 정의하였다.
그러므로, 루트 노드를 반환할 때까지 배열을 타고 올라가서 루트 노드를 반환하도록 하였다.
void SetParents(const int& _Left, const int& _Right)
{
int LeftParents = GetRootParents(_Left);
int RightParents = GetRootParents(_Right);
if (LeftParents < RightParents)
{
Parents[RightParents] = LeftParents;
}
else
{
Parents[LeftParents] = RightParents;
}
}
이 함수가 union역할을 하는 함수이다.
루트노드를 확인하며 부모 노드를 수정해주면 된다.
다음은 아래와 같이 반복문을 돌며 부모 노드를 설정해주면 끝이다.
for (int i = 0; i < NumOfLinkInfo; i++)
{
SetParents(Links[i].first, Links[i].second);
}
입력값에 대한 부모 노드 배열의 값을 확인해보자.
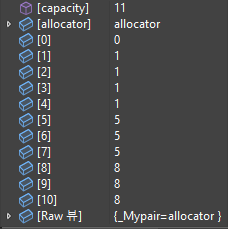
이와 같이 정확하게 저장되어 있음을 알 수 있다.
하지만, 똑같은 연결 관계더라도 입력을 아래와 같이 바꾼다면 어떨까.
10
7
4 3
2 1
1 4
7 6
5 6
9 10
9 8
결과는 아래와 같다.
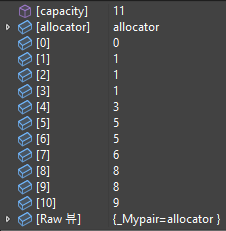
이를 시각화 해보자.

이런 모양이 된다.
즉, 입력에 따라 아주 비효율적인 트리구조를 구성할 수도 있게 되는 것이다.
이를 최적화하기 위해 사용하는 몇가지 기법이 더 있는 것으로 알고 있는데, 그 부분에 대해선 본인도 찾아봐야 할 듯 하다.
관련 게시글을 추후에 올려보도록 하겠다.
'C++ > 알고리즘' 카테고리의 다른 글
| 알고리즘 - 세그먼트 트리 (구간의 합 구하기) (0) | 2024.04.12 |
|---|---|
| 알고리즘 - 에라토스테네스의 체 (소수 판별) (0) | 2024.04.09 |
| 알고리즘 - 유클리드 호제법 (두 수의 최대 공약수 구하기) (0) | 2024.04.08 |
| 알고리즘 - CCW (세 점의 방향 판별하기) (0) | 2024.04.07 |
| 알고리즘 - LCA (최소 공통 조상 탐색) (0) | 2024.04.06 |