만약, 1~100까지의 숫자가 있을 때 그 사이에 있는 구간의 합을 구하고 싶다고 해보자.
예를 들면, 66~80의 합을 구하고 싶다거나 31~99의 합을 구하고 싶을 수도 있다.
이렇게 숫자가 간단하면 등차수열 공식을 이용하여 빠르게 구하면 된다.
그런데 숫자가 , 1, 6, 11, 12 ,18, 23,91 이런 식으로 규칙성 없이 주어진다면?
이 땐, 직접 더해볼 수 밖에 없다.
하지만, 더하는 것이 단 1번이라면 몰라도 여러 구간의 합을 계속 구해야 한다면?
불규칙적인 숫자가 100만개가 주어졌다고 해보자.
여기서, 랜덤한 구간의 합을 구하는 명령을 1만번정도 실행해야 한다고 하면, 구간의 길이만큼의 반복문을 1만번 실행해야 한다.
만약, 구간이 1~1000000 인 입력만 계속 들어온다면?
100억번의 반복문을 돌아야 한다 .
정말 끔찍한 연산량이다.. 이러한 시간복잡도를 줄이고 효율적으로 구간의 합을 구하기 위한 알고리즘이 세그먼트 트리이다.
세그먼트 트리
세그먼트 트리는 구간의 합을 미리 저장해놓고, 저장해놓은 값을 기반으로 빠르게 구간의 합을 탐색하는 알고리즘이다.
이름이 세그먼트 트리인 만큼 트리구조를 이용하여 구간의 합을 저장한다.
먼저, 아래의 배열과 같은 숫자가 주어졌다고 해보자.

여기서, 세그먼트 트리는 아래와 같이 구간을 나눠 합을 미리 저장하게 된다.

루트 노드엔 모든 숫자의 합을 저장하게 되고, 그 중 절반을 나눠 왼쪽 노드와 오른쪽 노드에 저장하게 된다.
말단까지 가면, 숫자 1개만큼의 합을 가진 노드가 위치하게 된다.
이렇게 저장한 뒤, 찾고자 하는 구간을 입력받으면 해당 구간에 대해 탐색하게 된다.
탐색 과정은 아래와 같다.

이렇게, 구간을 쪼개서 세그먼트 트리 내부에 저장된 구간의 합을 탐색하게 된다.
원리 자체는 이게 끝이다. 간단하다. 숫자 범위가 좁아서 연산 횟수가 별 차이가 안나는 것 처럼 보이지만,
실제로는 O(LogN)의 시간복잡도를 보유하기 때문에 선형으로 구간의 합을 구할 때보다 압도적으로 빠른 속력을 보인다.
다만, 구간의 합을 나눠서 미리 저장하는 만큼 메모리 사용량이 다소 많아지게 된다.
일반적으로 세그먼트 트리는 배열을 이용하기 때문에, 몇개의 구간합을 보유하는지에 대한 예측이 필요하다.
(reserve, resize를 사용하기 위해)
일반적으로 N개의 숫자가 주어지면, 4 *N으로 reserve, resize를 진행하게 된다.
그 이유는 아래와 같다. (수학적 증명이 필요없다면, 스킵해도 된다.)
N개의 숫자에 대해 아래의 등식이 성립한다고 가정해보자.
$$ 2^n <= N < 2^ {n + 1} $$
이 경우, 절반씩 나누어지는 세그먼트 트리의 특성을 생각하며 등비수열의 합 공식을 사용하면 구간합의 개수 M에 대해 아래와 같은 등식이 성립하게 된다.
$$ 2^ {n +1} + 1 <= M < 2^ {n + 2} $$
두 등식을 합쳐보면, 아래와 같은 등식으로 다시 표현할 수 있다.
$$2^n <= N < 2^{n + 1}< 2^{n + 1} + 1 <= M < 2^{n + 2}$$
마지막 항인 2^ (n + 2)는 4 * 2^n으로 풀어쓸 수 있기 때문에, 다시 아래와 같이 표현해보자.
$$2^n <= N < 2^ {n + 1} < 2^ {n + 1} + 1 <= M < 4 * 2^n $$
위에서 정의한 N의 범위를 생각해보면, 아래와 같은 등식까지 유도할 수 있다.
$$2^n <= N < 2^{n+1} < 2^{n+1} + 1 <= M < 4 * 2^n <= 4N$$
결과적으로 구간합의 개수 M에 대해 아래와 같은 관계가 성립하게 된다.
$$ M < 4N $$
세그먼트 트리는 일반적으로 3가지의 함수를 구현하게 된다.
1. 세그먼트 트리 초기화
2. 구간합 탐색
3. 숫자 변경에 대한 트리 업데이트
1번은 세그먼트 트리를 사용하기 위래 트리에 구간합을 저장하는 것이며,
2번은 원하는 구간을 입력하여 구간합을 구하는 함수이다.
3번은 무슨 말인지 잘 이해가 안될 수 있으니 설명해보겠다.
최초에 1,2,3,4,5 가 주어진다면 세그먼트 트리는 이 숫자를 기반으로 구간합을 저장할 것이다.
그런데, 중간에 세번째 숫자를 6으로 바꾸게 된다면?
1,2,6,4,5로 숫자가 변경되면 세그먼트 트리에 저장된 구간합을 수정할 필요가 있다.
3번은 이렇게 숫자를 중간에 변경할 경우 세그먼트 트리에 저장된 구간합을 갱신하는 함수를 의미한다.
이제 코드를 구현해 보겠다.
코드 구현

위와 같은 숫자 배열에 대해 구간합을 구한다고 가정하도록 하겠다.
std::vector<int> Nums;
std::vector<int> SegmentTree;
int main()
{
int NumSize = 8;
Nums.resize(NumSize + 1);
SegmentTree.resize(4 * NumSize);
Nums[1] = 1;
Nums[2] = 3;
Nums[3] = 4;
Nums[4] = 6;
Nums[5] = 8;
Nums[6] = 11;
Nums[7] = 13;
Nums[8] = 16;
return 0;
}
숫자의 개수를 저장하고, 이를 기반으로 숫자를 담을 배열과 세그먼트 트리의 사이즈를 resize하였다.
주의할 점은 0번 인덱스가 아닌 1번 인덱스부터 사용한다는 것이다.
배열을 이용해 트리를 구현하게 되면, 인덱스의 곱을 통해 부모자식관계를 맺게 되는데 0번 인덱스부터 시작하면 모든 인덱스가 0이 되어 버린다.
이제, SegmentTree를 초기화 하는 함수를 세워보자.
먼저 아래 그림을 보자.

현재 우리가 아는 정보는 말단 노드에 단일 숫자들이 저장될 것이라는 것이다.
그렇다면, 밑에서부터 올라오며 합을 기록해야 할텐데 문제는 말단 노드의 인덱스를 알지 못한다는 것이다.
처음부터 아래에서 위로 올라가며 구간합을 더하는 것은 불가능하기 때문에, 재귀함수를 이용해서 말단 노드까지 내려간 다음 말단 노드에서 다시 합을 해주며 위로 올라올 것이다.
int InitTree(int _Start, int _End, int _CurIndex)
{
if (_Start == _End)
{
SegmentTree[_CurIndex] = Nums[_Start];
return SegmentTree[_CurIndex];
}
int Mid = (_Start + _End) / 2;
int Left = InitTree(_Start, Mid, _CurIndex * 2);
int Right = InitTree(Mid + 1, _End, _CurIndex * 2 + 1);
SegmentTree[_CurIndex] = Left + Right;
return SegmentTree[_CurIndex];
}
보자. 파라미터의 _Start는 합을 구하고자 하는 구간의 시작지점이고 _End는 합을 구하고자 하는 구간의 끝지점이다.
_CurIndex는 SegmentTree의 인덱스이다.
아래쯤을 보면 Mid를 기준으로 Left와 Right를 나눈 뒤, 두 값을 더해 SegmentTree에 저장해주고 있다.
Left와 Right를 구하는 과정에서 구간을 계속 절반으로 쪼개고 있는데, 계속 쪼개다 보면 구간의 시작과 끝이 같아지는 지점이 온다.
이 때가 바로 말단노드인 것이다. _Start == End가 되는 지점에 Nums의 [_Start]를 SegmentTree에 저장해준 뒤 해당 값을 반환해주고 있다.
이 때부터, 위로 올라오며 구간합을 갱신하게 된다.
처음에는 InitTree(1, 8, 1)을 호출할 것이다.
_Start와 _End는 모든 숫자를 포함하는 구간으로 설정하고 _CurIndex는 1번 인덱스로 설정할 것이다.
이렇게 되면 루트노드부터 내려오며 모든 구간에 대한 구간합을 갱신하게 된다.

모두 끝나면 위 그림과 같은 값이 배열에 들어가 있을 것이다.

내부의 값을 보면 동일하게 들어있는 것을 확인할 수 있다.
SegmentTree의 초기화는 끝났다.
이제 구간합을 탐색하는 함수를 만들어보자.
int GetSum(int _NumStart, int _NumEnd, int _SegStart, int _SegEnd, int _CurIndex)
{
if (_SegStart > _NumEnd || _SegEnd < _NumStart)
{
return 0;
}
else if(_SegStart <= _NumStart && _SegEnd >= _NumEnd)
{
return SegmentTree[_CurIndex];
}
int _NumMid = (_NumStart + _NumEnd) / 2;
return GetSum(_NumStart, _NumMid, _SegStart, _SegEnd, _CurIndex * 2) + GetSum(_NumMid + 1, _NumEnd, _SegStart, _SegEnd, _CurIndex * 2 + 1);
}
_NumStart와 _NumEnd는 노드에 기록된 구간이고, _SegStart와 _SegEnd는 합을 구하고자 하는 구간이다.
먼저, 두 가지의 예외처리를 주었다.

이렇게, _NumStart ~ _NumEnd 와 _SegStart~_SegEnd가 전혀 겹치지 않을 땐 0을 반환하도록 하였다.

위와 같이, 인자로 받은 _SegStart와 _SegEnd가 _NumStart와 _NumEnd를 품고있는 상황이 된다면
그대로 SegmentTree[_CurIndex]를 반환하도록 하였다.
이렇게, 두 가지 예외처리를 설정한 뒤 재귀호출을 하였다.
재귀호출은 InitTree와 유사하게 Mid를 둔 뒤, 양 방향으로 나누어 탐색하였다.
_SegStart, _SegEnd는 그대로 두고 _NumStart, _NumEnd만 쪼개가며 탐색을 하였다.
과정을 하나하나 보며 어떻게 진행되나 보자.

이건, 루트노드의 왼쪽 자식 노드를 탐색하는 과정이다.
위에서 _SegStart, _SegEnd와 _NumStart, _NumEnd 범위가 아예 겹치지 않는 경우와 그 안에 포함되는 경우 두 가지에 대해 재귀호출 종료 조건을 달았다.
하얀색 배경으로 칠해진 노드는 범위가 겹치지 않아 0을 반환하고 있는 노드이며
검은색 배경으로 칠해진 노드는 _NumStart와 _NumEnd를 포함하고 있어 SegmentTree[_CurIndex]를 반환하는 경우이다.
주황색 노드는 _NumStart와 _NumEnd가 일부분만 겹쳐있는 노드이다.
2~6에 대한 구간합을 구하기 위해 재귀호출을 했더니, 왼쪽 자식 노드에서는 2~4의 구간합을 반환하고 있다.
오른쪽 자식 노드에 대해서도 보자.

동일하게 진행되지만, 오른쪽 노드는 말단노드에 도착하기 전에 예외처리가 되어, 말단 노드까지 가기 전에 답을 찾아냈다.
오른쪽 노드에선 5~6의 구간합을 반환하고 있다.
마지막으로 루트 노드에서 왼쪽 자식노드에서 구한 구간합 (2~4)와 오른쪽 자식 노드에서 구한 구간합(5~6)을 더한 (2 ~6)의 구간 합을 반환하게 되면, 찾고자 했던 2~6의 구간합을 구할 수 있게 된다.
이번엔, 중간에 숫자가 변경되는 경우 구간합을 갱신하는 Update함수를 만들어보겠다.
void Update(int _NumStart, int _NumEnd, int _NumIndex, int _AddValue, int _CurIndex)
{
if (_NumIndex < _NumStart || _NumIndex > _NumEnd)
{
return;
}
SegmentTree[_CurIndex] += _AddValue;
if (_NumStart == _NumEnd)
{
return;
}
int Mid = (_NumStart + _NumEnd) / 2;
Update(_NumStart, Mid, _NumIndex, _AddValue, _CurIndex * 2);
Update(Mid + 1, _NumEnd, _NumIndex, _AddValue, _CurIndex * 2 + 1);
}
이번에도 거의 유사하다.
_NumStart, _NumEnd는 노드가 저장하고 있는 구간 합의 구간이며, _NumIndex는 바뀐 숫자의 인덱스이다.
여기서 주의할 점은 _Addvalue이다.
만약, Nums[5] =3 에서 Nums[5] = 10 으로 바뀌었다면, _AddValue는 7이 된다.
Nums[5] = 10에서 Nums[5] = 3이 되었다면, _Addvalue는 -7이 된다.
이 함수는 숫자의 변화량만큼 구간합에 그대로 더해주는 방식이기 때문에 _Addvalue에는 바뀐 숫자를 넣는 것이 아니라 기존의 숫자와의 차이를 넣어주어야 한다.
_CurIndex는 SegmentTree의 인덱스이다.
먼저, _NumIndex를 _NumStart, _NumEnd가 포함하지 않는 경우에는 바로 Return 해주었다.
포함되었다면, SegmentTree에 _AddValue를 더해주어 구간합을 갱신해준다.
_NumStart와 _NumEnd가 같다면 (말단 노드라면) 이대로 끝내면 되고,
말단 노드가 아니라면 자식 노드에 대해서도 검사해야 한다.
자식노드에 대해 왼쪽 오른쪽 Update함수를 호출해주면 된다.
여기서, Update함수를 왼쪽과 오른쪽에 대해 둘 다 호출하고 있는데, _NumIndex는 둘 중 하나에밖에 속하지 못하기 때문에 둘 다 호출할 필요는 없다.
조건문을 달아서 한 쪽만 호출하게 할 수도 있지만, 어차피 양쪽의 함수를 호출해도 한쪽은 가장 위의 조건문 때문에 바로 return된다.
조건문을 다는 것보다 간단하기 때문에 위처럼 양쪽 노드의 update를 모두 호출하고 있다.
본인이 조건문을 달아서 한 쪽만 호출하게 하고 싶다면 그렇게 하면 된다.
이제 기능은 모두 구현하였다.
테스트 한 번 해보자.
InitTree는 위에서 확인하였으니 GetSum과 Update에 대해 확인해보자.

2~5의 구간합은 21이다.

3~8의 구간합은 58이다.

1~3의 구간합은 8이다.

잘 작동하는 것을 확인할 수 있다.
다음은 Update이다.

이렇게 4번 인덱스를 10으로 바꿔보겠다.
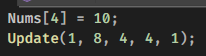
이렇게 갱신을 한 뒤 SegmentTree의 값을 확인해보자.

제대로 갱신된 것을 확인할 수 있다.
'C++ > 알고리즘' 카테고리의 다른 글
| 알고리즘 - 라인 스위핑 (0) | 2024.04.21 |
|---|---|
| 알고리즘 - 펜윅 트리 (구간의 합 구하기) (0) | 2024.04.13 |
| 알고리즘 - 에라토스테네스의 체 (소수 판별) (0) | 2024.04.09 |
| 알고리즘 - 유니온 파인드 (노드의 집합 판별하기) (0) | 2024.04.09 |
| 알고리즘 - 유클리드 호제법 (두 수의 최대 공약수 구하기) (0) | 2024.04.08 |