어느 게임 개발자의 기록

스터디를 진행하며 실시한 모의 면접을 정리한 내용입니다.
겹치는 내용을 고려하지 않고 면접을 실시하기 때문에 일자 별로 겹치는 내용이 많을 수 있습니다.

1. 가비지 컬렉션이란?

2. 가비지 컬렉션의 단점은? 

3. 힙과 우선순위 큐의 차이는?

4. 클래스, 객체, 인스턴스의 차이는?

5. push_back과 emplace_back의 차이는?

6. 코루틴과 멀티스레드의 차이는?

7. 앵커란 무엇인가? (언리얼엔진)

8. 객체 지향이란?

9. 메시와 머티리얼에 대해 설명하라.

10. 렌더링 파이프라인의 전체적인 과정에 대해 설명하라.

11. 오브젝트 풀링이란?

12. 반투명한 물체를 처리하는 방법은?

13. UDP 와 TCP 의 차이에 대해 설명하라.

14. 상속을 사용하는 이유는?

15. 템플릿과 오버로딩의 차이는?

16. 오버로딩과 오버라이딩의 차이는?

17. 스마트포인터란?

18. 32비트 , 64비트 운영체제 차이

19. 유저 영역 vs 커널 영역

20. 가상메모리란?

21. 페이징 기법이란?

23. 변환색인버퍼란?

22. 세그멘테이션 기법이란?

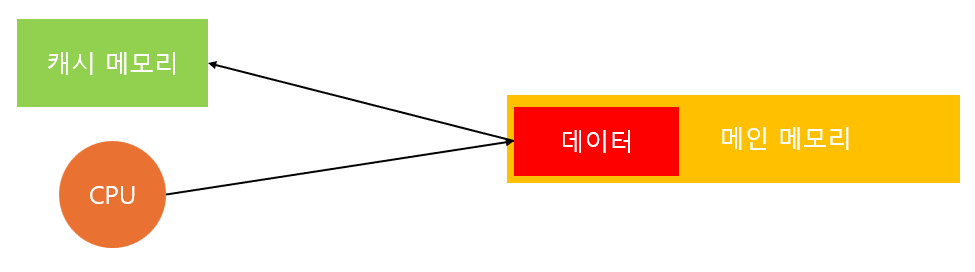
24. 캐시 메모리란?

25. 캐시적중률이란?

26. volatile 키워드란?

27. inline 키워드란?

28. 함수 뒤에 붙는 const 를 설명하라.

29. L-Value와 R-Value를 설명하라.

30. this 콜이란?

31. 멀티 스레드와 멀티 프로세스에 대해 설명하라.

32. 뮤텍스와 세마포어의 차이는?

33. IPC란?

34. unnamed PIPE vs named PIPE

35. IP와 MAC 이란?

36. IPv4 과 IPv6의 차이는?

37. 포트넘버란?

38. 프로세스의 메모리 구조를 설명해라.

39. 문자열 리터럴은 L-Value인가 R-Value인가?

40. 무브 시맨틱이란?

41. 플레이어를 기준으로 몬스터가 어디에 있는지 알아내는 방법

42. 행렬연산을 사용하는 이유는 무엇인가?

43. 노말맵이란?

44. 탄젠트 스페이스란?

45. G버퍼란?

46. AABB충돌이란? 문제점은?

47. OBB충돌이란?

48. 드로우콜이란?

49. 드로우콜 최적화는 CPU최적화인가 GPU최적화인가

50. 쿼터니언이란?

51. 짐벌락이란?

52. 픽셀충돌을 사용하는 이유는?

53. 싱글톤 패턴이란?

54. 멀티스레드 환경에서 싱글톤의 문제점

55. 전방선언이란 무엇인가? 사용하는 이유는?

56. 네임맹글링이란?

57.다중상속의 문제점

58. 라운드 로빈 알고리즘이란?

59. 컨텍스트 스위칭이란

60. 가상 소멸자를 쓰는 이유는 무엇인가?

61. 클래스와 구조체의 차이는?

62. RTTI란?

63. 람다함수란 무엇인가? 장단점은 무엇이 있는가?

64. string과 string_view의 차이

65. RTV란?

 

상자엔 익은 토마토와 익지 않은 토마토가 있다.

하루가 지나면 익은 토마토 주위 4방향에 있는 익지 않은 토마토는 익는다.

모든 토마토가 익을 때까지 시간이 얼마나 걸릴까?

문제 풀이

배열에 토마토의 정보를 담고 (전체 순회 -> 토마토 정보 업데이트 -> 모두 익었나 확인)의 과정을 반복하면 쉽게 해결할 수 있다. 본인이 해결한 방법은 약간 다르다. 익은 토마토의 위치를 모두 queue에 삽입한 뒤, 하나씩 뽑으며 BFS 방식으로 문제를 해결하였다.

풀이 코드

struct Data
{
    std::pair<int, int> Pos;
    int Days = 0;
};

먼저, queue에 삽입할 데이터 구조체를 만들어주었다.

익은 토마토의 위치와 며칠째에 익었는지를 저장하는 구조체이다.

int Width = 0;
int Height = 0;

std::cin >> Width >> Height;

std::vector<std::vector<int>> Map(Height, std::vector<int>(Width, 0));
std::queue<Data> Grown;

for (int i = 0; i < Height; i++)
{
    for (int j = 0; j < Width; j++)
    {
        std::cin >> Map[i][j];

        if (Map[i][j] == 1)
        {
            Grown.push({ { i, j }, 0 });
        }
    }
}

다음은 입력을 받아주었다.

입력을 받으면서 익은 토마토는 queue에 따로 삽입해주었다.

std::vector<int> DirX = { 1, 0, -1, 0 };
std::vector<int> DirY = { 0, 1, 0, -1 };

int Answer = 0;

while (Grown.size() > 0)
{
    Data CurData = Grown.front();
    Grown.pop();

    Answer = std::max(Answer, CurData.Days);

    for (int i = 0; i < 4; i++)
    {
        std::pair<int, int> NearTomato = { CurData.Pos.first + DirY[i], CurData.Pos.second + DirX[i]};

        if (NearTomato.first < 0 || NearTomato.second < 0 || NearTomato.first >= Height || NearTomato.second >= Width)
        {
            continue;
        }

        if (Map[NearTomato.first][NearTomato.second] == 0)
        {
            Map[NearTomato.first][NearTomato.second] = 1;
            Grown.push({ NearTomato, CurData.Days + 1});
        }
    }
}

다음은 BFS 구현코드이다.

먼저, 익은 토마토 하나를 꺼내서 주변 4방향에 익지 않은 토마토가 있나 검사한 뒤, 있다면 해당 토마토를 다시 queue에 삽입해주었다. 토마토가 익으려면 하루가 지나므로 Days에 +1을 해서 삽입해주었다.

Answer은 답을 저장할 변수인데 이 값은 계속 갱신해주었다.

for (int i = 0; i < Height; i++)
{
    for(int j = 0; j < Width; j++)
    {
        if (Map[i][j] == 0)
        {
            std::cout << -1;
            return 0;
        }
    }
}

std::cout << Answer;

return 0;

마지막에 아직 익지 않은 토마토가 있나 검사한 뒤, 있다면 -1을 출력하고 없다면 Answer 을 출력하도록 해주었다.

코드 전문

#include <iostream>
#include <set>
#include <queue>
#include <vector>

void Init()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
}

struct Data
{
    std::pair<int, int> Pos;
    int Days = 0;
};

int main()
{
    Init();

    int Width = 0;
    int Height = 0;

    std::cin >> Width >> Height;

    std::vector<std::vector<int>> Map(Height, std::vector<int>(Width, 0));
    std::queue<Data> Grown;

    for (int i = 0; i < Height; i++)
    {
        for (int j = 0; j < Width; j++)
        {
            std::cin >> Map[i][j];

            if (Map[i][j] == 1)
            {
                Grown.push({ { i, j }, 0 });
            }
        }
    }

    std::vector<int> DirX = { 1, 0, -1, 0 };
    std::vector<int> DirY = { 0, 1, 0, -1 };

    int Answer = 0;

    while (Grown.size() > 0)
    {
        Data CurData = Grown.front();
        Grown.pop();

        Answer = std::max(Answer, CurData.Days);

        for (int i = 0; i < 4; i++)
        {
            std::pair<int, int> NearTomato = { CurData.Pos.first + DirY[i], CurData.Pos.second + DirX[i]};

            if (NearTomato.first < 0 || NearTomato.second < 0 || NearTomato.first >= Height || NearTomato.second >= Width)
            {
                continue;
            }

            if (Map[NearTomato.first][NearTomato.second] == 0)
            {
                Map[NearTomato.first][NearTomato.second] = 1;
                Grown.push({ NearTomato, CurData.Days + 1});
            }
        }
    }

    for (int i = 0; i < Height; i++)
    {
        for(int j = 0; j < Width; j++)
        {
            if (Map[i][j] == 0)
            {
                std::cout << -1;
                return 0;
            }
        }
    }

    std::cout << Answer;

    return 0;
}

스터디를 진행하며 실시한 모의 면접을 정리한 내용입니다.
겹치는 내용을 고려하지 않고 면접을 실시하기 때문에 일자 별로 겹치는 내용이 많을 수 있습니다.

1. 깊이 버퍼와 스텐실 버퍼란?

2. std::function과 C스타일 함수 포인터의 차이

3. 얕은 복사와 깊은 복사

4. 컨텍스트 스위칭이란?

5.  멀티스레드 프로그래밍이 유리한 경우는?

6. 빅 앤디언 방식과 비교했을 때, 리틀 앤디언 방식의 장점

7. 그래픽스 행렬 변환 중 W 나누기를 실행하는 단계는 어디인가?  W를 나누는 이유는?

8. 추상 클래스란?

9. 코루틴이란?

10. Pawn 과 Character의 차이 (언리얼 엔진)

11. C++ 타입 캐스팅의 종류

12. 부동소수점이란?

13. 템플릿을 사용하는 이유와 장단점에 대해 설명하라.

14. 매크로 함수와 인라인 함수의 차이

15. 시스템 콜이란?

16. 빌드 과정에 대해 설명하라.

17. 포워드 렌더링과 디퍼드 렌더링에 대해 설명하라.

18. 네임스페이스란?

19. 포인터를 사용하는 이유

20. 벡터의 외적과 내적

21. 로컬 좌표와 월드 좌표에 대해 설명하라.

22. 포인터와 참조자의 차이

23. RAII 패턴에 대해 설명하라.

24. virtual을 생성자에 붙이지 않는 이유는?

25. 절차지향과 객체지향에 대해 설명하라.

26. 임계영역이란?

27. 직렬화와 역직렬화에 대해 설명하라.

28. 프리컴파일헤더란? 장단점은?

29. FSM과 행동트리의 장단점은?

30. 더블버퍼링 기법에 대해 설명하라.

31. 뮤텍스와 스핀락의 차이

32. 트라이 자료구조에 대해 설명하라.

간만에 재밌게 한 게임!

소울라이크 특유의 느낌을 가장 잘 살린 게임인듯?

회차 플레이를 선호하지는 않지만 다음에 2회차도 한 번 해봐야겠다. 진엔딩이 궁금해졌다

STL에선 벡터, 리스트, 맵, 셋, 해시 맵 등 다양한 자료구조를 제공해준다. 

그 중에서 벡터와 리스트는 자주 비교되는 자료구조이다. 두 자료구조의 차이를 알아보자.

std::vector

std;:vector는 배열 기반의 자료구조이다. 배열 기반인 만큼 모든 데이터가 메모리 상에 연속적으로 위치한다.

벡터의 특징은 대부분 메모리에 연속적으로 위치한다는 특성에서 시작된다.

먼저, 벡터는 임의 접근(random access)이 가능하다. 임의 접근이란 쉽게 말해서 원하는 원소에 바로 접근하는 것이다.

std::vector<int> Arr;

for(int i = 0; i < 10; i++)
{
    Arr.push_back(i);
}

위 코드와 같이 Arr이라는 벡터에 10개의 원소를 삽입했다고 해보자.

이 때, 5번째의 원소에 접근하고 싶다면, Arr[4]와 같이 인덱스를 통해 접근할 수 있다. 

(인덱스는 0번부터 시작하므로 5번째 원소는 4번 인덱스에 위치하게 된다.)

왜 이런 접근이 가능할까? 원소가 위치하는 주소를 특정할 수 있기 때문이다.

배열은 선언되면, 배열의 시작점을 주소값으로 보유하게 된다.

1번 원소 = 시작주소

2번 원소 = 시작 주소 + 원소의 메모리 크기

3번 원소 = (시작 주소 + 원소의 메모리 크기 * 2)

모든 원소의 메모리 크기는 일정하기 때문에, 위와 같은 방식으로 원소의 위치를 특정할 수 있는 것이다.

인덱스가 0번부터 시작하는 이유도 이 때문이다.

시작 주소 + (인덱스 * 원소의 메모리 크기) 의 공식을 세우려면 인덱스가 0부터 시작해야 하기 때문이다.

이처럼 데이터가 메모리에 연속적으로 위치한다는 특성 덕분에, 높은 캐시적중률을 자랑하기도 한다.

(캐시 적중률을 모른다면 여기를 참고)

하지만, 메모리에 연속적으로 위치한다는 특성때문에 몇 가지 문제점도 발생한다.

먼저 원소의 삽입과 삭제에 있어서 추가적인 연산이 발생한다는 것이다.

특정 원소를 삭제하게 되면, 배열 안에 비어있는 공간이 발생하게 된다. 이 빈 공간을 메꾸지 않으면 해당 인덱스에 접근할 때 어떤 오류가 발생할지 예측할 수 없으며 메모리 연속적이라는 특성도 사라지게 된다.

이로 인해, 벡터는 중간의 데이터를 삭제할 경우 모든 원소를 앞으로 끌어오게 된다. 이 과정에서 추가적인 연산이 발생하게 된다. 중간에 데이터를 삽입할 때에도 마찬가지이다. 원소를 모두 뒤로 밀어내야 하기 때문에 추가적인 연산이 발생하게 된다.

원소의 개수가 많아질수록 삽입 삭제 연산이 무거워지고 오버헤드가 커질 것이다.

두 번째 문제는 데이터를 메모리에 연속적으로 위치하게 하기 위해서,메모리 공간을 미리 확보해야 한다는 것이다. 10개의 원소를 삽입하려면 원소의 크기 * 10만큼 메모리 공간이 존재해야 하며 그 만큼을 선점해야 한다.

그런데, 메모리 공간은 원소 10개의 크기만큼만 확보하였는데 11번째 원소가 삽입된다면 어떻게 될까?

일반적인 배열의 경우엔 아예 불가능한 연산이지만, 벡터는 새롭게 메모리 공간을 동적으로 할당한 뒤 기존의 데이터를 모두 옮기고 기존의 메모리 영역을 해제하는 방식으로 해결한다. 즉, 기존에 할당한 메모리 공간보다 더 큰 공간을 필요로 하게 되면 메모리 할당 -> 데이터 복사 -> 메모리 해제의 과정을 거치므로 아주 커다란 오버헤드가 발생하게 된다.

이를 해결하기 위해선 어떻게 해야할까? 메모리 크기를 충분히 크게 할당해놓는 것이다. 벡터엔 reserve라는 멤버함수가 존재한다. 이 reserve를 통해 미리 충분한 크기의 메모리를 할당한 뒤에 그 범위 안에서 사용하게 되면, reserve를 호출할 때 메모리 할당 -> 데이터 복사 -> 메모리 해제의 연산을 1번 실행하고 이후에는 추가적으로 실행되지 않는다.

(할당해놓은 범위를 넘어서지 않는다는 조건 하에)

하지만, 메모리를 너무 많은 크기로 할당해놓게 되면 메모리 내부 단편화가 발생하므로 어느 정도의 메모리가 필요한지 미리 예측해놓고 필요한 만큼만 할당하는 것이 중요하다.

벡터의 특징을 정리해보자.

핵심 : 데이터가 메모리에 연속적으로 위치한다.

장점 1 : 임의 접근이 가능하다.

장점 2 : 캐시 적중률이 매우 높다.

단점 1 : 삽입, 삭제에 추가적인 연산이 필요하다.

단점 2 : 동적 할당과 데이터 이동으로 인한 오버헤드를 줄이기 위해 메모리를 미리 할당해야 한다.

(사실 Reserve, Resize 등의 함수를 한 번만 호출하면 되기 때문에 단점이라고 하기 애매하긴 하다.) 

std::list

std::list는 포인터 기반의 자료구조이다.

백터는 미리 메모리를 할당해 놓고, 그 안에서 순차적으로 데이터를 저장하는 반면 list는 새로운 원소가 추가될 때마다 새롭게 동적 할당을 하여 포인터로 이전의 원소와 연결하는 과정으로 데이터를 저장하게 된다.

이러한 특성 때문에, list는 데이터의 삽입과 삭제가 간단하다.

 새로운 원소를 추가하게 되면, 메모리를 동적으로 할당한 뒤에 포인터만 연결하는 과정을 거치면 되기 때문에, 원소가 어느 위치에 삽입되더라도 데이터를 뒤로 밀거나 앞으로 당기는 등의 추가적인 연산이 필요하지 않게 된다.

또한, 원소가 추가되는 만큼만 동적으로 할당하기 때문에 벡터처럼 미리 메모리를 할당해놓을 필요가 없고, 메모리 내부 단편화 또한 발생하지 않는다.

하지만, 원소가 추가될 때마다 계속 동적 할당을 실행하기 때문에 원소의 삽입 자체가 벡터에 비해 낮은 성능을 보이게 된다. 또한, 데이터가 메모리에 연속적으로 위치하지 않기 때문에 캐시 적중률 또한 매우 낮은 편이다. 

그 뿐만이 아니라, 포인터로 연결되어 있다는 특성 때문에 특정 원소의 주소값을 바로 유추할 수가 없어 임의 접근이 불가능하다. 첫 번째 원소부터 포인터를 타고 가며 접근하는 순차 접근만 가능하다.

리스트의 특징을 정리해보자.

핵심 : 데이터가 메모리에 연속적으로 위치하지 않고, 포인터를 이용해 논리적으로 연결되어 있다. 

장점 1 : 삽입, 삭제가 간단하다.

장점 2 : 메모리를 미리 할당할 필요가 없다. 

단점 1 : 임의 접근이 불가능하다.

단점 2 : 원소가 삽입될 때마다 동적 할당의 오버헤드가 발생한다.

단점 3 : 캐시 적중률이 매우 낮다.

삽입 삭제는 list가 vector보다 더 유리할까?

삽입, 삭제 연산을 빅오 표기법으로 표현하면 std::vector의 시간 복잡도는 O(n)이며, std::list의 시간 복잡도는 O(1)이다. 이 때문에, 리스트의 장점을 인터넷에서 찾아보면 삽입 삭제가 빠르다는 말이 항상 나온다.

하지만, 실제로는 그렇다고 단정지을 수는 없다. 

std::vector가 std::list에 비해 삽입 삭제가 느리다고 말하는 이유는 std::vector에선 데이터를 삽입, 삭제할 때 데이터를 뒤로 밀거나 앞으로 당기는 추가적인 연산이 필요하고, std::list에선 그러한 과정이 필요하지 않기 때문이다.

하지만 생각해보면 std::list는 데이터를 삽입, 삭제할 때 메모리를 할당하거나 해제하는 과정이 필요하다.

즉, std::list에서도 삽입, 삭제 시에 포인터만 끊고 연결하는 것이 아니라 메모리의 할당과 해제라는 추가적인 연산이 필요하다는 것이다.

그러므로 std::vector와 std::list의 삽입 삭제의 연산 속도를 비교하려면 원소를 앞으로 당기거나 뒤로 미는 연산 속도와 동적 할당, 메모리 해제의 속도를 비교해야 하는 것이다. 

또한, 시간 복잡도는 항상 최악의 경우만을 가정하지만, 실무에선 최악의 경우만 발생하는 것이 아니기 때문이다.

최선의 경우만 발생하는 로직에서도 과연 list가 vector보다 유리할까?

이를 직접 비교해보도록 하겠다.

#include <vector>
#include <list>
#include <iostream>
#include <chrono>

int main()
{
	std::vector<int> Vector;
	Vector.reserve(1000);

	std::list<int> List;
	
	{
		std::chrono::system_clock::time_point InsertStart = std::chrono::system_clock::now();

		for (int i = 0; i < 1000; i++)
		{
			Vector.insert(Vector.begin(), i);
		}

		std::chrono::system_clock::time_point InsertEnd = std::chrono::system_clock::now();
		std::chrono::nanoseconds VectorInsertDuration = std::chrono::duration_cast<std::chrono::nanoseconds>(InsertEnd - InsertStart);

		std::cout << "VectorInsertDuration : " << VectorInsertDuration << std::endl;

		std::chrono::system_clock::time_point EraseStart = std::chrono::system_clock::now();

		for (int i = 0; i < 1000; i++)
		{
			Vector.erase(Vector.begin());
		}

		std::chrono::system_clock::time_point EraseEnd = std::chrono::system_clock::now();
		std::chrono::nanoseconds VectorEraseDuration = std::chrono::duration_cast<std::chrono::nanoseconds>(EraseEnd - EraseStart);

		std::cout << "VectorEraseDuration : " << VectorEraseDuration << std::endl;
	}

	{
		std::chrono::system_clock::time_point InsertStart = std::chrono::system_clock::now();

		for (int i = 0; i < 1000; i++)
		{
			List.insert(List.begin(), i);
		}

		std::chrono::system_clock::time_point InsertEnd = std::chrono::system_clock::now();
		std::chrono::nanoseconds ListInsertDuration = std::chrono::duration_cast<std::chrono::nanoseconds>(InsertEnd - InsertStart);

		std::cout << "ListInsertDuration : " << ListInsertDuration << std::endl;

		std::chrono::system_clock::time_point EraseStart = std::chrono::system_clock::now();

		for (int i = 0; i < 1000; i++)
		{
			List.erase(List.begin());
		}

		std::chrono::system_clock::time_point EraseEnd = std::chrono::system_clock::now();
		std::chrono::nanoseconds ListEraseDuration = std::chrono::duration_cast<std::chrono::nanoseconds>(EraseEnd - EraseStart);

		std::cout << "ListEraseDuration : " << ListEraseDuration << std::endl;
	}
}

위는 1000개의 원소를 삽입, 삭제하는 속도를 비교하는 코드이다.

벡터에서 최악의 경우를 확인하기 위해 가장 앞에 원소를 삽입, 삭제하도록 하였다.

삽입,삭제 속도만을 비교하기 위해 reserve는 미리 해주었다.

1000개의 원소에 대한 결과는 아래와 같다.

최악의 경우임에도 불구하고 vector가 list에 비해 속도가 앞서는 것을 볼 수 있다.

10000개의 원소에 대해서도 체크해보자.

10000개로 원소가 늘어나니 list가 두 배 이상 앞서는 것을 볼 수 있다.

하지만, 벡터의 삽입 삭제를 맨 뒤에서 하도록 하면 어떨까?

위는 1000개의 원소에 대한 것이고, 아래는 10000개의 원소에 대한 것이다.

최선의 경우엔 벡터가 list보다 압도적으로 빠른 것을 알 수 있다.

원소의 개수가 많아질수록 최악의 경우엔 삽입, 삭제가 list가 훨씬 유리하다고 볼 수 있지만 최선의 경우엔 list가 vector보다 훨씬 빠른 것을 알 수 있다. 즉, 삽입 삭제가 list가 vector보다 항상 유리하냐고 한다면 답은 아니라는 것이다.

특정 로직에 사용할 자료구조를 선택할 때, 삽입 삭제가 자주 발생한다는 이유로 list를 선택하는 것은 정답이 아니다. 

현재 내가 구현하고 있는 로직이 어느 위치에서 삽입, 삭제가 자주 발생하는지 혹은 원소의 개수는 어느정도인지 파악한 뒤에 사용하는 것이 중요하다. 

또한 캐시 적중률의 차이로 순회의 경우 벡터가 압도적으로 빠르기 때문에, 삽입, 삭제 여부만 판단하는 것이 아니라 순회의 속도도 고려해야 한다. 아래는 10000개 원소의 순회 속도이다.

벡터 vs 리스트

두 자료구조의 차이를 표로 정리해보겠다.

CPU는 컴퓨터를 구성하는 하드웨어중에서 가장 빠른 작업 처리 속도를 가지고 있다. 반면, 메인 메모리는 CPU에 비해 매우 낮은 작업 처리 속도를 가지고 있다.

두 하드웨어간의 속도 차이 때문에, CPU에서 메인 메모리에 직업 접근을 하게 되면 CPU에선 병목 현상이 발생하게 된다.

메인 메모리에 접근하여 데이터를 얻어오는 작은 작업의 시간이 CPU에선 수도 없이 많은 명령어를 처리할 수 있는 시간이기 때문이다.

이를 해결하기 위해 존재하는 것이 캐시메모리이다.

캐시 메모리

CPU는 필요한 데이터를 가져오기 위해서 메인 메모리에 접근을 할 수 밖에 없다. 하지만, 그 횟수를 최소화하기 위해 캐시 메모리를 사용하게 된다. CPU에서 메모리의 특정 주소에 접근하게 되면 그 주소를 시작으로 일정 크기만큼의 데이터를 한 번에 가져와 캐시 메모리에 저장하게 된다.

캐시 메모리는 메인 메모리에 비해 속력이 매우 빠르기 때문에, CPU에선 캐시 메모리에서 데이터를 탐색하는 것이 훨씬 효율적이기 때문이다.

하지만, 캐시 메모리는 메인 메모리에 비해 용량이 매우 작기 때문에 필요한 데이터가 캐시 메모리에 없을 경우 CPU는 다시 메인 메모리에 접근하여 캐시 메모리의 데이터를 새로 갱신하게 된다. 위에서 말했듯이, 메인 메모리에 접근하는 것은 성능상 손해가 크기 때문에 최소화하는 것이 좋다. 그렇다면, 캐시 메모리에 원하는 데이터가 최대한 많이 있을수록 메인 메모리에 접근하는 횟수가 적어질 것이며 성능의 손해를 최소화할 수 있을 것이다.

이 것을 캐시 적중률이라고 한다.

캐시 적중률

캐시 메모리에 현재 A,B,C,D,E,F 이렇게 6개의 데이터가 있다고 해보자.

CPU에서 A, B, C, X 이렇게 4개의 데이터를 필요로 한다면, A,B,C는 캐시 메모리에서 찾을 수 있지만, X의 경우엔 캐시 메모리에서 찾을 수가 없다.

이 경우, A,B,C 의 경우 캐시 적중이라고 표현하며, X에 대해선 캐시 미스(miss)라고 표현하게 된다.

캐시 적중이 얼마나 많이 발생하는가를 캐시 적중률이라고 표현하는 것이다.

그렇다면, 캐시 미스가 최대한 적게 발생해야 메인 메모리에 접근해서 캐시 메모리를 새로 채우는 과정이 적게 발생할 것이며 성능상 손해가 적게 될 것이다. 즉, 캐시 적중률이 높을수록 성능상 손해를 적게 보고 있다고 말할 수 있는 것이다.

그렇다면, 캐시 적중률을 높이기 위해선 어떻게 해야할까?

캐시 적중률을 높이는 법

방법은 간단하다. 관련된 데이터를 메모리에 연속적으로 위치하게 하면 된다. 캐시 메모리를 채우는 방식은 CPU가 메인 메모리에 접근한 주소를 시작으로 특정 크기만큼 연속적으로 가져오는 방식이기 때문이다.

예를 들어, 특정 자료구조의 원소를 순회한다고 해보자. 1번째 원소와 2번째 원소가 메모리 상에서 먼 위치에 있다면, 각 원소에 접근할 때마다 캐시를 새로 채워야 하는 상황이 발생할 수 있다. 반면, 모든 원소가 순차적으로 붙어있다면 자료구조의 원소가 캐시 메모리에 존재할 가능성이 매우 높아지며, 캐시 적중률을 최대로 높일 수 있는 것이다.

이 때문에 배열과 리스트의 성능 차이가 발생한다. 배열은 그 구조상 모든 데이터가 메모리에 연속적으로 위치하게 되지만, 리스트의 경우 모든 원소가 동적으로 할당되어 포인터로 연결되어 있기 때문에 메모리의 다양한 위치에 분산되어 있다. 그렇기 때문에, 동일한 시간 복잡도의 연산이라도 배열 기반의 자료구조가 포인터 기반의 자료구조보다 일반적으로 우수한 성능을 보이게 된다.

배열 뿐만이 아니라 메모리 풀링 또한 캐시 적중률을 높이는데 도움이 될 수 있다. 미리 메모리를 할당해놓고 필요한 만큼 가져다 쓰는 방식이기 때문에, 모든 데이터가 메모리 상에 연속적으로 위치하게 된다. 메모리 풀링은 캐시 적중률을 높일 뿐만 아니라 메모리 외부 단편화를 해결하는 데도 큰 도움이 되기 때문에 잘 활용하면 성능상 큰 이점을 얻을 수 있을 것이다.

 

특정 마을에서 파티가 열린다고 했을 때, 모든 학생은 본인이 사는 마을에서 파티가 열리는 마을로 갔다가 다시 원래 마을로 돌아올 것이다.

이 때, 사는 마을 -> 파티 마을 -> 사는 마을의 경로를 통해 이동하게 될 것이다.

이 경로를 통해 이동할 때, 가장 큰 시간을 소비하는 학생의 소요 시간을 출력하면 된다.

모든 길은 단방향이기 때문에, 사는 마을 -> 파티 마을로 갈 때 소요되는 시간과 파티 마을 -> 사는 마을로 갈 때 소요되는 시간은 서로 다를 수 있다는 것을 주의해야 한다.

문제 풀이

먼저, 이 문제는 다익스트라를 이용하면 쉽게 해결할 수 있다.

사는 마을 -> 파티 마을로 가는 경로에 대해 다익스트라 알고리즘을 적용하여 최소 비용을 구하고,

파티 마을 -> 사는 마을로 가는 경로에 대해 다익스트라 알고리즘을 적용하여 최소 비용을 구할 수 있다.

두 경우의 비용을 더해서 각 학생의 소요 시간을 구할 수 있을 것이다.

다만, 입력으로 주어진 값을 평범하게 다익스트라 알고리즘을 적용하게 되면 시간초과가 발생할 수 있다.

왜냐하면, 1번 마을을 시작점으로 다익스트라 알고리즘을 수행해야 하고, 2번 마을을 시작점으로 다익스트라 알고리즘을 수행해야 하고, N번 마을까지 모두 다익스트라 알고리즘을 수행해야 한다.

파티 마을에서 원래 마을로 돌아올 떄엔 시작점이 파티 마을로 고정이므로 1번의 다익스트라로 해결할 수 있지만, 기존의 마을에서 파티 마을로 가는 경우에는 마을의 개수만큼 다익스트라 알고리즘을 수행해야 할 것이다.

하지만, 주어진 입력을 뒤집는다면 한 번의 다익스트라를 통해 답을 구할 수 있게 된다.

예를 들어, 5개의 마을이 있고 5번 마을에서 파티가 열린다고 해보자.

1번 마을 -> 5번 마을 : 비용 5

2번 마을 -> 5번 마을 : 비용 3

이렇게 입력이 주어진다면,

5번 마을 -> 1번 마을 : 비용 5

5번 마을 -> 2번 마을 : 비용 3 

이렇게 마을의 시작점과 도착점을 뒤집어서 저장하는 것이다.

이 문제에선 특정 마을에서 파티 마을을 향해 가는 경로의 방향이 중요한 것이 아니라 비용이 중요한 것이므로 뒤집어서 파티 마을 -> 특정 마을로 해석해도 문제가 발생하지 않을 것이다.

그러므로, 입력을 그대로 저장한 뒤 파티 마을을 시작점으로 다익스트라 알고리즘을 1번 수행하고 입력을 반대로 저장한 뒤 파티 마을을 시작점으로 다익스트라 알고리즘을 1번 수행하게 되면 총 2번의 다익스트라 알고리즘으로 답을 구할 수 있게 되는 것이다.

코드 풀이

void Dijk(std::vector<int>& _Cost, std::vector<std::vector<std::pair<int, int>>>& _Link, int _StartNode)
{
    std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int>>, std::greater<std::pair<int, int>>> Queue;
    
    Queue.push({ 0, _StartNode });

    while (Queue.size() > 0)
    {
        int CurNode = Queue.top().second;
        int CurCost = Queue.top().first;

        Queue.pop();

        if (_Cost[CurNode] < CurCost)
        {
            continue;
        }

        for (int j = 0; j < _Link[CurNode].size(); j++)
        {
            int NextNode = _Link[CurNode][j].second;
            int NextCost = _Link[CurNode][j].first;

            int NextCostSum = CurCost + NextCost;

            if (NextCostSum < _Cost[NextNode])
            {
                _Cost[NextNode] = NextCostSum;
                Queue.push({ NextCostSum, NextNode });
            }
        }
    }
}

다익스트라 알고리즘 구현 코드이다. 우선 순위 큐를 활용하여 구현하였다.

int NumMan = 0;
int NumRoad = 0;
int PartyNode = 0;

std::cin >> NumMan >> NumRoad >> PartyNode;

std::vector<std::vector<std::pair<int, int>>> Link(NumMan);
std::vector<std::vector<std::pair<int, int>>> ReverseLink(NumMan);

for (int i = 0; i < NumRoad; i++)
{
    int Start = 0;
    int End = 0;
    int Cost = 0;
    
    std::cin >> Start >> End >> Cost;

    Link[Start - 1].push_back({ Cost, End - 1});
    ReverseLink[End - 1].push_back({ Cost, Start - 1 });
}

위에서 말했던 것처럼 정방향으로 입력을 저장하고, 역방향으로도 입력을 저장해주었다.

std::vector<int> Costs(NumMan, INT_MAX);
std::vector<int> ReverseCosts(NumMan, INT_MAX);

다익스트라를 사용해 갱신할 비용 배열도 정방향, 역방향 2개를 만들어주었다.

Dijk(Costs, Link, PartyNode - 1);
Dijk(ReverseCosts, ReverseLink, PartyNode - 1);

정방향, 역방향으로 다익스트라를 1번씩 수행해 주었다.

int MaxCost = -1;

Costs[PartyNode - 1] = 0;
ReverseCosts[PartyNode - 1] = 0;

for (int i = 0; i < NumMan; i++)
{
    int CurCost = Costs[i] + ReverseCosts[i];
    MaxCost = std::max(MaxCost, CurCost);
}

std::cout << MaxCost;

return 0;

정방향 비용은 파티 마을 -> 시작 마을의 비용이며 역방향 비용은 시작 마을 -> 파티 마을의 비용이다.

두 비용을 합한 값이 가장 큰 값을 구해주었고, 그 값을 출력해주었다.

여기서 중요한 것은 파티가 시작되는 마을의 값을 0으로 초기화해주어야 한다는 것이다.

다익스트라 알고리즘을 수행하게 되면, 파티 마을도 의도치 않게 비용이 갱신될 수 있으므로 반드시 제외해주어야 한다.

문제 풀이

#include <iostream>
#include <vector>
#include <queue>
#include <climits>

void Init()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
}

void Dijk(std::vector<int>& _Cost, std::vector<std::vector<std::pair<int, int>>>& _Link, int _StartNode)
{
    std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int>>, std::greater<std::pair<int, int>>> Queue;
    
    Queue.push({ 0, _StartNode });

    while (Queue.size() > 0)
    {
        int CurNode = Queue.top().second;
        int CurCost = Queue.top().first;

        Queue.pop();

        if (_Cost[CurNode] < CurCost)
        {
            continue;
        }

        for (int j = 0; j < _Link[CurNode].size(); j++)
        {
            int NextNode = _Link[CurNode][j].second;
            int NextCost = _Link[CurNode][j].first;

            int NextCostSum = CurCost + NextCost;

            if (NextCostSum < _Cost[NextNode])
            {
                _Cost[NextNode] = NextCostSum;
                Queue.push({ NextCostSum, NextNode });
            }
        }
    }
}

int main()
{
    Init();

    int NumMan = 0;
    int NumRoad = 0;
    int PartyNode = 0;
    
    std::cin >> NumMan >> NumRoad >> PartyNode;
    
    std::vector<std::vector<std::pair<int, int>>> Link(NumMan);
    std::vector<std::vector<std::pair<int, int>>> ReverseLink(NumMan);

    for (int i = 0; i < NumRoad; i++)
    {
        int Start = 0;
        int End = 0;
        int Cost = 0;
        
        std::cin >> Start >> End >> Cost;

        Link[Start - 1].push_back({ Cost, End - 1});
        ReverseLink[End - 1].push_back({ Cost, Start - 1 });
    }

    std::vector<int> Costs(NumMan, INT_MAX);
    std::vector<int> ReverseCosts(NumMan, INT_MAX);

    Dijk(Costs, Link, PartyNode - 1);
    Dijk(ReverseCosts, ReverseLink, PartyNode - 1);

    int MaxCost = -1;

    Costs[PartyNode - 1] = 0;
    ReverseCosts[PartyNode - 1] = 0;

    for (int i = 0; i < NumMan; i++)
    {
        int CurCost = Costs[i] + ReverseCosts[i];
        MaxCost = std::max(MaxCost, CurCost);
    }

    std::cout << MaxCost;

    return 0;
}

 

규칙에 맞게 게임을 했을 때, 플레이어의 점수를 예측하는 문제이다.

A의 카드 숫자가 B의 카드 숫자로 나누어진다면 A의 패배, B의 승리이며 B의 카드 숫자가 A의 카드 숫자로 나누어진다면 A의 승리, B의 패배이다.

문제 풀이

한 쪽의 숫자가 다른 한 쪽의 숫자로 나누어진다면 승패가 결정나는 게임이기 때문에, 배수관계를 통해 승패를 파악할 수 있다. 하지만, 최대 10만명의 플레이어가 참가한 상황에서 모든 플레이어간의 대결 경우를 계산하게 되면 50억번의 경우를 계산해야한다. 

이를 해결하기 위해, 플레이어가 가진 숫자에 접근하여 계산하는 것이 아니라 숫자 자체의 존재 여부를 파악하도록 하였다. 무슨 말이냐면, 입력받은 플레이어의 카드 숫자 배열 외에 100만개의 boolean 배열을 만들어 인덱스에 해당하는 숫자가 있는지를 저장하는 배열을 하나 만들었다는 의미이다.

예를 들어, (2, 4, 6, 8)의 카드가 현재 플레이어들이 보유하고 있는 카드라면, boolean 배열 A에서 A[2] = true, A[4] = true, A[6] = true, A[8] = true 인 것이다. 이를 제외한 나머지 모든 값은 false이다.

이렇게 값을 별도로 저장한 이유는 연산 횟수를 줄이기 위해서이다. 플레이어 간의 대결을 이중 반복문으로 구현하여 모든 대결을 하게 되면, N^2의 시간복잡도를 가진 연산을 해야한다. 반면, 위의 boolean 배열을 통해 대결을 하면 NlogN의 시간복잡도를 보유하게 된다. 뭐가 다른지 아래 식을 통해 보자.

//플레이어간의 대결을 하는 경우
for(int i = 0; i < 플레이어의 수; i++)
{
    for(int j = i + 1; j < 플레이어의 수; j++)
    {
        //대결
    }
}

//boolean배열을 통해 숫자끼리 대결을 하는 경우
std::vector<bool> Array(1000001);

for(int i = 0; i < 플레이어의 수; i++)
{
    int Num = 플레이어의 카드 숫자;
    
    for(int j = Num * 2; j < 1000001; j += Num)
    {
        if(Array[j] == true)
        {
            //대결
        }
    }
}

두 방식의 차이는 내부에 있는 반복문의 차이이다.

위에선 모든 플레이어에 대해 반복문을 돌고 있다. j를 1씩 증가하면 반복문을 돌기 때문에 10만명의 플레이어가 있다고 했을 땐 99999 + 99998 + 99997 + 99996 .... + 1 번의 반복문을 돌게 될 것이다. 대략 50억번의 반복문을 돌게 된다.

반면, 아래의 방식은 j를 Num씩 증가시키며 배수에 대해서만 체크하고 있기 때문에, 1000000 + 500000 + 333333 + 250000 + 200000 + 133333 ..... + 1 번의 반복문을 돌게 된다. 대략 1400만번의 반복문을 돌게 된다.

이를 통해, 숫자간의 대결을 진행한 뒤, 점수를 저장해야 하는데 플레이어의 카드 숫자 배열에선 해당 숫자로 접근할 수가 없다. (다시 순차탐색 과정을 거쳐야 하는데, 그렇게 하면 결국 시간초과가 발생할 수 밖에 없게 된다.)

그러므로, 점수를 저장할 배열을 하나 더 만들어 주어야 한다.

boolean 배열과 동일하게 1000000개의 원소를 저장하도록 배열을 만들어서 각 인덱스에 맞는 숫자의 점수를 저장하면 된다.

코드 풀이

int PlayerSize = 0;
std::cin >> PlayerSize;

std::vector<int> PlayerNums(PlayerSize);
std::vector<bool> isExist(1000001);
std::vector<int> Score(1000001);

for (int i = 0; i < PlayerSize; i++)
{
    std::cin >> PlayerNums[i];
    isExist[PlayerNums[i]] = true;
}

입력과 초기화이다.

먼저, Player의 수를 입력받은 뒤 그 수에 맞게 PlayerNum을 생성하였고, 각 플레이어의 카드 숫자를 입력받아주었다. 

isExist는 해당 숫자가 있는가를 저장하는 배열이며, Score는 점수를 저장하는 배열이다.

isExist는 플레이어의 점수를 저장한 뒤, 바로 값을 갱신해주었다.

for (int i = 0; i < PlayerSize; i++)
{
    int CurNum = PlayerNums[i];

    for (int i = CurNum * 2; i < 1000001; i += CurNum)
    {
        if (isExist[i] == true)
        {
            Score[CurNum]++;
            Score[i]--;
        }
    }
}

탐색과정이다.

먼저, 현재 플레이어의 숫자를 기준으로 그 배수에 대해 모두 탐색하였다.

CurNum의 배수가 존재하는 숫자라면, 대결을 실행하였다.

대결은 항상 나의 점수 + 1, 상대방의 점수 -1로 끝난다. (상대방의 숫자가 나의 숫자의 배수이기 때문에)

for (int i = 0; i < PlayerSize; i++)
{
    std::cout << Score[PlayerNums[i]] << " ";
}

return 0;

모든 대결이 끝난 뒤, 각 플레이어의 카드 숫자에 해당하는 Score의 값을 출력해주면 된다.

코드 전문

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>

void Init()
{
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);
	std::cout.tie(nullptr);
}

int main()
{
    Init();

    int PlayerSize = 0;
    std::cin >> PlayerSize;

    std::vector<int> PlayerNums(PlayerSize);
    std::vector<bool> isExist(1000001);
    std::vector<int> Score(1000001);
    
    for (int i = 0; i < PlayerSize; i++)
    {
        std::cin >> PlayerNums[i];
        isExist[PlayerNums[i]] = true;
    }

    for (int i = 0; i < PlayerSize; i++)
    {
        int CurNum = PlayerNums[i];

        for (int i = CurNum * 2; i < 1000001; i += CurNum)
        {
            if (isExist[i] == true)
            {
                Score[CurNum]++;
                Score[i]--;
            }
        }
    }

    for (int i = 0; i < PlayerSize; i++)
    {
        std::cout << Score[PlayerNums[i]] << " ";
    }

    return 0;
}

각 학생들이 싫어하는 사람의 목록이 주어졌을 때, 모든 학생이 싫어하는 사람과 같은 팀이 되지 않도록 팀을 배분하면 된다.

5
1 3
1 5
2 1 4
1 3
1 2

위와 같이 입력이 주어진다면 아래와 같이 여러개의 정답이 나올 수 있다.

백팀 : 1, 2, 4 / 청팀 : 3, 5

백팀 : 3, 5 / 청팀 : 1, 2, 4

백팀 : 1, 4, 5 / 청팀 : 2, 3

백팀 : 2, 3 / 청팀 : 1, 4, 5

(실제로는 더 있을 수도 있다.)

이 중, 하나의 경우를 구한 뒤 출력하면 된다.

문제 풀이

각 학생들이 싫어하는 학생의 목록을 확인한 뒤, 하나씩 팀에 배분해주면 된다.

위에서 보여주었던 입력에 대해 생각해보자.

1번 학생은 3번 학생을 싫어한다.

=> 청팀 : 1 / 백팀 : 3

2번 학생은 5번 학생을 싫어한다.

=> 청팀 : 1, 2 / 백팀 : 3, 5 

3번 학생은 1번 학생, 4번 학생을 싫어한다.

=> 청팀 : 1, 2, 4 / 백팀 : 3, 5 

4번 학생은 3번 학생을 싫어한다.

=> 청팀 : 1, 2, 4 / 백팀 : 3, 5 (이미 팀 배분이 되어 있어, 변화가 없다.)

5번 학생은 2번 학생을 싫어한다.

=> 청팀 : 1, 2, 4 / 백팀 : 3, 5 (이미 팀 배분이 되어 있어, 변화가 없다.)

이렇게, 선택된 학생이 싫어하는 학생의 목록을 기반으로 팀에 차례대로 배분해주면 된다.

풀이 코드

std::vector<std::vector<int>> Hates;

std::vector<bool> isDevided;

//-1이면 청, 1이면 백
std::vector<int> DevidedTeam;

std::vector<int> BlueTeam;
std::vector<int> WhiteTeam;

먼저, 이렇게 5개의 벡터를 선언해주었다.

Hates는 인덱스에 해당하는 학생이 싫어하는 학생들의 목록을 저장한 벡터이다.

isDevided는 인덱스에 해당하는 학생이 싫어하는 학생들을 팀에 배분했는가를 담고 있는 벡터이다.

DevidedTeam은 학생들의 현재 팀을 저장한 벡터이다. 0이면 아직 팀 배분이 되지 않은 것이고, -1이면 청팀 1이면 백팀이다. 

BlueTeam과 WhiteTeam은 각각 팀에 포함된 학생들의 목록이다.

void Recursive(int _CurIndex)
{
    if (isDevided[_CurIndex] == true)
    {
        return;
    }

    isDevided[_CurIndex] = true;
    
    if (DevidedTeam[_CurIndex] == 0)
    {
        DevidedTeam[_CurIndex] = -1;
    }

    for (int i = 0; i < Hates[_CurIndex].size(); i++)
    {
        int CurHateIndex = Hates[_CurIndex][i];

        if (DevidedTeam[CurHateIndex] != 0)
        {
        	continue;
        }

        DevidedTeam[CurHateIndex] = -DevidedTeam[_CurIndex];
        
        Recursive(CurHateIndex);
    }
}

학생들이 현재 싫어하는 목록을 학생의 반대 팀에 배치한 뒤, 배치된 학생을 기준을 기준으로 함수를 재귀적으로 호출하여 다시 해당 학생이 싫어하는 학생들을 모두 반대 팀에 배치하도록 하였다.

싫어하는 학생을 배치한 학생의 인덱스에 대해 isDevided 를 true로 만들어, 같은 학생에 대해 여러 번 실행되지 않도록 하였다.

isDevided.resize(NumMan, false);
DevidedTeam.resize(NumMan, 0);

for (int i = 0; i < NumMan; i++)
{
    Recursive(i);
}

위의 함수를 모든 학생에 대해 실행하였다.

BlueTeam.reserve(NumMan);
WhiteTeam.reserve(NumMan);

for (int i = 0; i < NumMan; i++)
{
    if (DevidedTeam[i] == -1)
    {
        BlueTeam.push_back(i + 1);
    }
    else if (DevidedTeam[i] == 1)
    {
        WhiteTeam.push_back(i + 1);
    }
}

std::cout << BlueTeam.size() << "\n";

for (int i = 0; i < BlueTeam.size(); i++)
{
    std::cout << BlueTeam[i] << " ";
}

std::cout << "\n";
std::cout << WhiteTeam.size() << "\n";

for (int i = 0; i < WhiteTeam.size(); i++)
{
    std::cout << WhiteTeam[i] << " ";
}

학생들이 배치된 팀에 따라, 각 벡터에 삽입하였고, 해당 벡터의 사이즈와 원소를 모두 출력해주었다.

코드 전문

#include <iostream>
#include <vector>

void Init()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
}

std::vector<std::vector<int>> Hates;

std::vector<bool> isDevided;

//-1이면 청, 1이면 백
std::vector<int> DevidedTeam;

std::vector<int> BlueTeam;
std::vector<int> WhiteTeam;

void Recursive(int _CurIndex)
{
    if (isDevided[_CurIndex] == true)
    {
        return;
    }

    isDevided[_CurIndex] = true;

    if (DevidedTeam[_CurIndex] == 0)
    {
        DevidedTeam[_CurIndex] = -1;
    }

    for (int i = 0; i < Hates[_CurIndex].size(); i++)
    {
        int CurHateIndex = Hates[_CurIndex][i];

        if (DevidedTeam[CurHateIndex] != 0)
        {
            continue;
        }

        DevidedTeam[CurHateIndex] = -DevidedTeam[_CurIndex];

        Recursive(CurHateIndex);
    }
}

int main()
{
    Init();

    int NumMan = 0;
    std::cin >> NumMan;

    Hates.resize(NumMan);

    for (int i = 0; i < NumMan; i++)
    {
        int NumHate = 0;
        std::cin >> NumHate;

        Hates[i].reserve(NumHate);

        for (int j = 0; j < NumHate; j++)
        {
            int HateMan = 0;
            std::cin >> HateMan;

            Hates[i].push_back(HateMan - 1);
        }
    }

    isDevided.resize(NumMan, false);
    DevidedTeam.resize(NumMan, 0);

    for (int i = 0; i < NumMan; i++)
    {
        Recursive(i);
    }

    BlueTeam.reserve(NumMan);
    WhiteTeam.reserve(NumMan);

    for (int i = 0; i < NumMan; i++)
    {
        if (DevidedTeam[i] == -1)
        {
            BlueTeam.push_back(i + 1);
        }
        else if (DevidedTeam[i] == 1)
        {
            WhiteTeam.push_back(i + 1);
        }
    }

    std::cout << BlueTeam.size() << "\n";

    for (int i = 0; i < BlueTeam.size(); i++)
    {
        std::cout << BlueTeam[i] << " ";
    }

    std::cout << "\n";
    std::cout << WhiteTeam.size() << "\n";

    for (int i = 0; i < WhiteTeam.size(); i++)
    {
        std::cout << WhiteTeam[i] << " ";
    }

    return 0;
}

 

 

N개의 앱이 켜있다고 해보자.

각 앱은 m_1, m_2, m_3....m_n의 메모리를 사용하고 있으며, 각 앱을 비활성화하게 되면 각 c_1, c_2, c_3, c_4...c_n의 비용이 발생하게 된다.

M바이트를 확보하기 위해, 임의의 앱을 비활성화 했을 때 발생하는 비용의 최소값을 구하자.

문제 풀이

문제 자체는 간단한 배낭 문제이다. 다만, 일반적인 배낭 문제와는 다르게 최소값을 구하는 문제이기 때문에 떠올리는 것이나 구현하는 것이 다소 어려울 수도 있었을 것 같다.

배낭문제는 보통 개수와 수치(무게, 비용 등)을 이용해서 2차원 배열을 구성하게 된다. 위의 문제에서 개수, 메모리를 이용해서 2차원 배열을 구성하게 되면 최대 1000000000개의 원소를 가지는 배열을 만들어야 하므로 메모리 초과가 발생할 수 밖에 없다. 그러므로 2차원 배열은 (개수, 비용)을 이용해서 구성할 것이다.

그렇다면, 배열의 원소는 어떤 값을 저장해야 할까?

문제에서 구하는 것은 M바이트를 확보하기 위한 최소 비용이다.

반대로, N의 비용을 사용했을 때 최대한으로 확보할 수 있는 메모리를 구하면 어떨까?

문제에서 주어진 최대 비용은 10000이다. (100개의 앱 * 100의 비용)

그러므로, N의 비용을 사용했을 때 최대한으로 확보할 수 있는 메모리를 배열에 저장한 뒤 0 ~ 10000 까지의 비용 중 확보할 수 있는 메모리가 입력값보다 큰 비용을 구한 뒤, 그 값의 최소를 출력하면 되는 것이다.

배열의 원소를 갱신하는 것은 일반 배낭 문제와 동일하게 하면 된다.

풀이 코드

int NumApp = 0;
int TargetMem = 0;

std::cin >> NumApp >> TargetMem;

std::vector<int> AppMemories(NumApp + 1, 0);
std::vector<int> AppCosts(NumApp + 1, 0);

for (int i = 1; i <= NumApp; i++)
{
    std::cin >> AppMemories[i];
}

for (int i = 1; i <= NumApp; i++)
{
    std::cin >> AppCosts[i];
}

먼저, 입력을 모두 받아주자.

앱의 개수와 확보할 메모리를 입력받은 뒤, 각 앱의 메모리 사용량과 비활성화시 발생하는 비용을 모두 저장해주었다.

std::vector<std::vector<int>> DP(NumApp + 1, std::vector<int>(10001, 0));

다음으로 배낭 문제 해결에 사용할 DP 배열을 만들어주었다.

발생할 수 있는 최대 비용은 10000이므로, 배열의 size를 위와 같이 만들어주었다.

for (int i = 1; i <= NumApp; i++)
{
    for (int j = 0; j <= 10000; j++)
    {
        if (j >= AppCosts[i])
        {
            DP[i][j] = std::max(DP[i - 1][j], DP[i - 1][j - AppCosts[i]] + AppMemories[i]);
        }
        else
        {
            DP[i][j] = DP[i - 1][j];
        }
    }
}

일반적인 배낭문제와 동일하게 반복문을 돌려주면 된다.

각 원소의 값은 i개의 앱을 비활성화하여 j의 비용이 발생했을 때 확보할 수 있는 최대 메모리양이다.

int Answer = 0;

for (int i = 0; i <= 10000; i++)
{
    if (DP[NumApp][i] >= TargetMem)
    {
        Answer = i;
        break;
    }
}

이후, i를 0부터 10000까지 반복문을 돌며 TargetMem을 확보할 수 있는 최소 비용을 구해주면 된다.

std::cout << Answer;

답을 출력해주면 된다.

코드 전문

#include <iostream>
#include <vector>
#include <algorithm>

void Init()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
}

int main()
{
    Init();

    int NumApp = 0;
    int TargetMem = 0;
    
    std::cin >> NumApp >> TargetMem;

    std::vector<int> AppMemories(NumApp + 1, 0);
    std::vector<int> AppCosts(NumApp + 1, 0);

    for (int i = 1; i <= NumApp; i++)
    {
        std::cin >> AppMemories[i];
    }

    for (int i = 1; i <= NumApp; i++)
    {
        std::cin >> AppCosts[i];
    }

    std::vector<std::vector<int>> DP(NumApp + 1, std::vector<int>(10001, 0));

    for (int i = 1; i <= NumApp; i++)
    {
        for (int j = 0; j <= 10000; j++)
        {
            if (j >= AppCosts[i])
            {
                DP[i][j] = std::max(DP[i - 1][j], DP[i - 1][j - AppCosts[i]] + AppMemories[i]);
            }
            else
            {
                DP[i][j] = DP[i - 1][j];
            }
        }
    }

    int Answer = 0;

    for (int i = 0; i <= 10000; i++)
    {
        if (DP[NumApp][i] >= TargetMem)
        {
            Answer = i;
            break;
        }
    }

    std::cout << Answer;

    return 0;
}