어느 게임 개발자의 기록

 

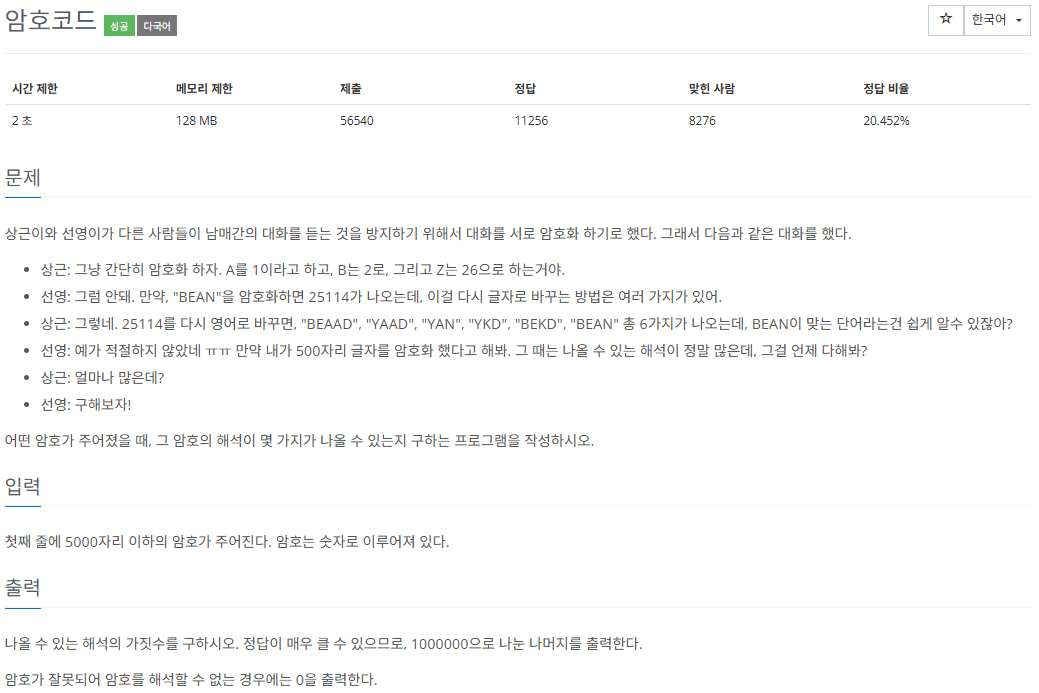
A = 1, B = 2, C = 3 ... Z = 26 등 알파벳을 각 순서와 동일한 숫자로 치환하여 새로운 숫자 문자열을 만든다.

해당 숫자 문자열을 다시 기존의 알파벳 문자열로 복호화하게 되면, 경우의 수가 하나가 아니라 여럿 존재할 수 있다.

예를 들어, 19의 경우 1 + 9 => AI 로 표현할 수도 있지만, 19 -> S 로 표현할 수도 있다.

이처럼, 숫자 문자열이 주어졌을 때 해석 가능한 알파벳 문자열의 경우의 수를 출력하면 된다.

주의할 점은 경우의 수가 매우 많으므로 1000000으로 나눠서 저장하도록 하자.

문제 풀이

DP를 이용하여 풀 수 있는 문제이다.

입력된 문자열을 순차적으로 탐색하며, 현재 가리키는 숫자가 1자리 숫자로 해석될 수 있는 경우와 2자리 숫자의 1의 자리로 해석될 수 있는 경우를 구해주면 된다.

이렇게 길이가 5인 문자열 "12345"가 주어졌다고 해보자.

"12345"의 부분 문자열인 "123"에 대해 경우를 생각해보자.

123은 위와 같이 3개의 경우를 가지며, 3개의 경우는 2개의 종류로 나누어 볼 수 있다.

1. 마지막 숫자가 한 자리수인 경우

2. 마지막 숫자가 두 자리수의 1의 자리인 경우

1번 경우를 살펴보자.

1번 경우는 마지막 3을 제외한 앞의 숫자들을 보면 규칙이 보인다.

12를 해석하는 경우의 수이다.

즉, 길이가 N인 문자열을 해석할 때, 마지막 숫자를 한자리 숫자라고 고려한다면

0 ~ (N - 1) 의 문자열을 해석하는 경우의 수와 동일하다는 것이다

2번 경우도 살펴보자.

2번 경우는 마지막 숫자가 두 자리수의 1의 자리라고 했기 때문에, 그 앞의 숫자는 두자리 숫자의 10의 자리가 된다.

1번 경우를 살필 때와 동일하지만, 이 번엔 두자리 숫자이므로 0 ~ (N - 2) 길이의 문자열을 해석하는 경우의 수와 동일하게 된다.

즉 DP(N)을 길이가 N인 문자열을 해석하는 경우의 수라고 한다면, DP(N) = DP(N - 1) + DP(N - 2)가 된다.

풀이 코드

std::string Encryption;
std::cin >> Encryption;

if (Encryption[0] == '0')
{
    std::cout << 0;
    return 0;
}

if (Encryption.size() == 1)
{
    std::cout << 1;
    return 0;
}

먼저 입력을 받아주었다.

이후, 맨 앞이 0으로 시작하거나 길이가 1인 경우에 대해 예외처리를 해주었다.

std::vector<int> DP(Encryption.size());
DP[0] = 1;

int FrontTwoNum = std::stoi(Encryption.substr(0, 2));
if (FrontTwoNum >= 10 && FrontTwoNum <= 26)
{
	DP[1] += 1;
}

if(Encryption[1] - '0' != 0) 
{
	DP[1] += 1;
}

다음은 DP배열을 선언해주었다.
DP[0]은 한자리 숫자로 해석되는 1가지 경우밖에 없기 때문에 1로 초기화할 수 있다.

DP[1]의 경우 두 가지를 고려할 수 있다.

12처럼 1 + 2, 12 이렇게 두가지로 해석되는 경우가 있고

27처럼 2 + 7로만 해석되는 경우가 있다.

그러므로, 앞자리 숫자와 현재숫자를 고려하여 두가지 경우로 해석될 수 있는 경우엔 DP[1]  = 2 로 초기화하였고, 아닌 경우엔 1로 초기화하였다.

for (int i = 2; i < Encryption.size(); i++)
{
    int CurNum = Encryption[i] - '0';
    int PrevNum = Encryption[i - 1] - '0';

    if ((PrevNum == 1 && CurNum <= 9) || (PrevNum == 2 && CurNum <=6))
    {
        DP[i] += DP[i - 2];
    }

    if (CurNum != 0)
    {
        DP[i] += DP[i - 1];
    }

    DP[i] %= 1000000;
}

그 다음은 반복문을 돌며 DP배열을 갱신해주었다.

만약, 현재 숫자와 앞의 숫자를 합한 두자리 숫자가 10~26 사이의 숫자로 해석될 수 있다면 DP[i -2]를 DP[i]에 더해주었으며, 1~9로 해석될 수 있는 경우에는 DP[i]를 더해주었다.

만약, 현재 숫자가 0이라면 한자리 숫자로는 해석될 수 없다.

경우의 수가 커지는 것을 방지하여 문제의 조건에 맞게 1000000으로 나누어서 저장해주자.

std::cout << DP[DP.size() - 1];

return 0;

DP의 마지막 원소를 출력해주면 문제 해결이다.

코드 전문

#include <iostream>
#include <vector>
#include <string>

void Init()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
}

int main()
{
    Init();

    std::string Encryption;
    std::cin >> Encryption;

    if (Encryption[0] == '0')
    {
        std::cout << 0;
        return 0;
    }

    if (Encryption.size() == 1)
    {
        std::cout << 1;
        return 0;
    }

    std::vector<int> DP(Encryption.size());
    DP[0] = 1;

    int FrontTwoNum = std::stoi(Encryption.substr(0, 2));
    if (FrontTwoNum >= 10 && FrontTwoNum <= 26)
    {
        DP[1] += 1;
    }
    
    if(Encryption[1] - '0' != 0) 
    {
        DP[1] += 1;
    }

    for (int i = 2; i < Encryption.size(); i++)
    {
        int CurNum = Encryption[i] - '0';
        int PrevNum = Encryption[i - 1] - '0';

        if ((PrevNum == 1 && CurNum <= 9) || (PrevNum == 2 && CurNum <=6))
        {
            DP[i] += DP[i - 2];
        }

        if (CurNum != 0)
        {
            DP[i] += DP[i - 1];
        }

        DP[i] %= 1000000;
    }

    std::cout << DP[DP.size() - 1];

    return 0;
}

발행 / 구독 패턴이란, 두 객체의 상호작용을 대리자를 통해 진행하는 패턴이다.

언리얼 엔진의 Delegate에도 사용되었다고 하며, 대표적인 객체지향 디자인 패턴 중 하나이다.

발행  구독 패턴

잡지사 A가 있다고 해보자.

몇몇 사람들은 잡지사 A의 신간이 발매되면, 해당 신간을 배송받기 위해 구독 서비스를 가입했다.

그렇다면, 잡지사 A는 신간이 발매되면 구독 서비스에 가입한 모든 사람들에게 잡지를 배송해야 한다.

이 과정을 코드로 구현해보자.

class Subscriber
{
public:
    void Read(int _Num)
    {
        std::cout << _Num << "번째 구독자는 신간 잡지를 읽었습니다." << std::endl;
    }
};

class Person1 : public Subscriber
{

};

class Person2 : public Subscriber
{
};

class MagazinePub
{
public:
    void ReleaseNewMagazine()
    {
        std::cout << "신간 잡지가 발매되었습니다." << std::endl;
        DeliverMagazine();
    }

    void DeliverMagazine()
    {
        for (int i = 0; i < Subs.size(); i++)
        {
            std::cout << i + 1 << "번째 구독자에게 신간 잡지를 배송했습니다." << std::endl;
            Subs[i].Read(i + 1);
        }
    }

    void AddSubScriber(Subscriber& _SubScriber)
    {
        Subs.push_back(_SubScriber);
    }

private:
    std::vector<Subscriber> Subs;
};

int main()
{
    MagazinePub Publisher;

    Person1 SubScriber1;
    Person2 SubScriber2;

    Publisher.AddSubScriber(SubScriber1);
    Publisher.AddSubScriber(SubScriber2);

    Publisher.ReleaseNewMagazine();

    return 0;
}

이런 식으로 구현할 수 있을 것이다.

Publisher는 모든 Subscriber를 자료구조에 저장한 뒤, 신간잡지가 발매되면 모든 SubScriber의 함수를 호출하는 것이다.

하지만, 이 방식은 좋은 방법이 아니다.

Publisher와 Subscriber는 서로 의존성이 생기며, 결합도가 높아진다.

또한, Publisher의 구독을 하려면 반드시 Subscriber 클래스를 상속받아야만 한다.

그렇다면, 이런 방법은 어떨까?

별도의 클래스를 하나 만들어놓은 뒤, 해당 클래스를 통해 Publisher 와 Subscriber가 소통하도록 하는 것이다.

예를 들어, 잡지사와 구독자 사이에 대행업체가 하나 생겼다고 가정해보자.

구독자는 대행업체를 통해, 구독 의사를 알리며 대행업체는 구독자들의 정보를 보관하게 된다.

잡지사는 신간이 발매되면, 대행업체에 신간 발매 소식을 전한 뒤 신간 잡지를 대행업체에 보내준다.

이후, 대행업체는 보유한 정보를 기반으로 모든 구독자들에게 신간 잡지를 뿌려주는 것이다.

이를 더 쉽게 이해하기 위해, 다른 예시를 하나 들어보겠다.

어떤 보스 몹이 소환되어 있다고 해보자. 해당 보스몹은 작은 몬스터 세마리를 소환하였다.

그리고, 보스몹이 사망하였다면 생존해있는 작은 몬스터 세마리도 함께 소멸해야 할 것이다.

이 때, 이를 구현하기 위해 일반적으로 생각할 수 있는 아이디어는 위에서 코드로 적은 것과 동일할 것이다.

작은 몬스터의 포인터를 모두 자료구조에 저장해놓은 뒤, 사망하는 순간 모든 작은 몬스터들의 사망 함수를 호출하는 것이다. 하지만, 위에서 말했듯이 이건 좋은 방법이 아니다.

모든 작은 몬스터의 자료형이 다르다면, 보스 몬스터는 모든 자료형을 알아야 할 것이며 인터페이스를 사용한다면 모든 작은 몬스터들이 이 한 번의 소통을 위해 인터페이스를 추가로 상속받아야 한다. 

이를 아래와 같은 방법으로 해결해보자

class Delegate
{
public:
    void Bind(std::function<void()> _Func)
    {
        Funcs.push_back(_Func);
    }

    void Execute()
    {
        for (int i = 0; i < Funcs.size(); i++)
        {
            Funcs[i]();
        }
    }

private:
    std::vector<std::function<void()>> Funcs;
};

먼저, 발행구독 패턴의 핵심인 Delegate를 보자.

내부에는 함수포인터를 저장한 배열이 있다.

그리고, 멤버함수에는 함수포인터를 자료구조에 추가하는 Bind 함수와, 모든 Funcs의 함수포인터를 실행하는 Execute가 있다.

이처럼, 함수포인터를 사용하여 외부에서 함수를 Funcs에 저장하기 때문에 자료형이 수만가지여도 Delegate는 손쉽게 대응할 수 있다.

//Subscriber
class MiniMob1
{
public:
    void Die()
    {
        std::cout << "MiniMob1 이 죽었습니다." << std::endl;
    }
};

//Subscriber
class MiniMob2
{
public:
    void Die()
    {
        std::cout << "MiniMob2 가 죽었습니다." << std::endl;
    }
};

//Subscriber
class MiniMob3
{
public:
    void Die()
    {
        std::cout << "MiniMob3 이 죽었습니다." << std::endl;
    }
};

작은 몬스터 3마리의 클래스를 이렇게 선언했다고 해보자.

각 Die함수들을 Delegate에 Bind해줄것이다.

//Publisher
class Boss
{
public:
    void SetDelegate(Delegate* _Delegate)
    {
        MyDelegate = _Delegate;
    }

    void Die()
    {
        std::cout << "Boss가 죽었습니다. " << std::endl;
        
        if (MyDelegate != nullptr)
        {
            MyDelegate->Execute();
        }
    }

private:
    Delegate* MyDelegate = nullptr;
};

그리고 보스 몬스터는 사망하는 순간 해당 델리게이트의 Execute를 호출함으로써 델리게이트에 Bind된 함수를 모두 실행해줄 것이다.

메인함수를 보자.

int main()
{
    Delegate NewDelegate;

    Boss NewBoss;

    MiniMob1 NewMob1;
    MiniMob2 NewMob2;
    MiniMob3 NewMob3;

    NewBoss.SetDelegate(&NewDelegate);
    
    NewDelegate.Bind(std::bind(&MiniMob1::Die, &NewMob1));
    NewDelegate.Bind(std::bind(&MiniMob2::Die, &NewMob2));
    NewDelegate.Bind(std::bind(&MiniMob3::Die, &NewMob3));

    NewBoss.Die();

    return 0;
}

델리게이트를 선언한 뒤, 작은 몹들은 델리게이트에 각 함수를 bind해주고 있다.

그리고 마지막에 보스의 Die가 호출되었다.

결과는 이렇다.

보스몹은 모든 작은 몬스터를 알지 못하고, 직접 함수를 호출해주지도 않았다.

하지만, 보스가 사망하는 순간 모든 작은 몬스터들도 사망한 것을 확인할 수 있다.

이처럼, Delegate 클래스와 같은 대리자를 별도로 두고 해당 클래스를 통해 소통하는 것이 발행 구독 패턴이다.

이로 인해, 보스몹과 작은 몬스터들은 결합도와 의존성이 매우 낮아지며, 객체지향적으로 더 완성도 있게 기능을 설계할 수 있게 된다.

그림으로 보면, 이런 관계가 형성되는 것이다.

이처럼, 중간에 대리자 클래스를 두어 서로 다른 클래스간의 소통을 대신 진행하는 패턴을 구독/발행 패턴이라고 한다.

현재, 오목에서 승리한 사람이 있는지 탐색하는 문제이다.

오목의 규칙 그대로, 5개의 연속된 바둑알을 놓은 사람이 있는지 판단하고 있다면 이긴 사람을 출력하고, 없다면 0을 출력하면 된다.

문제 풀이

바둑판 위에서 바둑알이 놓여있는 모든 위치에 대해,  5개의 바둑알이 연결되어 있는지를 검사하였다.

기본적으로는 이렇게, 8방향에 대해 오목이 5개가 연결되어 있는지를 검사해야 할 것이다.

하지만, 꼭 8방향을 다 검사할 필요는 없다.

왜냐하면, 모듬 점에 대해서 탐색을 진행하기 때문에, 기준점에서 오른쪽 아래로 검사하는 것은 다른 기준점에서 왼쪽 위를 검사하는 것과 같다. 

예를 들어, (1,1) 에서 오른쪽 아래 방향을 검사해서 오목이 나오지 않았다면, (1,1) (2,2) (3,3) (4,4) (5,5)는 연속으로 돌이 놓여있지 않은 상황이다.

이 때, 만약 (1,1) (2,2) (3,3)은 검은돌이고, (4,4)는 하얀돌이며 (5,5)는 검은 돌이라고 해보자.

이 때, (5,5)에서 왼쪽 위를 검사하는 것이 의미가 있을까?

(5,5)에서 왼쪽 위 방향으로 오목이 만들어져 있다면, 이미 (1,1)에서 탐지한 뒤 검사를 종료했을 것이다.

그러므로 모든 점을 기준으로 오른쪽 아래만 검사하면 된다.

동일한 이유로 모든 점에선 우측 상단, 우측, 우측 하단, 하단 이렇게 4방향에 대해서만 검사하면 된다.

이 4방향으로만 연속된 바둑알 5개가 놓여있는지 검사하였다.

풀이 코드

std::vector<std::vector<int>> Board(19, std::vector<int>(19, 0));
for (int i = 0; i < 19; i++)
{
    for (int j = 0; j < 19; j++)
    {
        std::cin >> Board[i][j];
    }
}

먼저 바둑판의 상태를 입력받았다.

for (int i = 0; i < 19; i++)
{
    for (int j = 0; j < 19; j++)
    {
        if (Board[i][j] == 0)
        {
            continue;
        }

        if (Check(Board, j, i) == true)
        {
            std::cout << Board[i][j] << "\n";
            std::cout << i + 1 << " " << j + 1;

            return 0;
        }
    }
}

std::cout << 0;

return 0;

이후, 모든 점에 대해 검사를 하였다. 

바둑알이 놓여있지 않은 점에 대해서는 continue해주었다.

만약, 해당 위치에서 오목이 발견되었다면, 해당 위치의 바둑알의 생상과 위치를 출력한 뒤 프로세스를 종료하였으며, 발견되지 않고 반복문들 탈출하였다면 0을 출력하도록 해주었다.

bool Check(const std::vector<std::vector<int>>& _Board, int _X, int _Y)
{
    int CurStone = _Board[_Y][_X];

    //우상
    if (!(_X - 1 >= 0 && _Y + 1 < 19 && _Board[_Y + 1][_X - 1] == CurStone))
    {
        int Count = 0;

        for (int i = 0; i < 19; i++)
        {
            int NextX = _X + i;
            int NextY = _Y - i;

            if (NextX >= 19 || NextY < 0)
            {
                break;
            }

            if (_Board[NextY][NextX] == CurStone)
            {
                Count++;
            }
            else
            {
                break;
            }
        }

        if (Count == 5)
        {
            return true;
        }
    }

    //우
    if (!(_X - 1 >= 0 && _Board[_Y][_X - 1] == CurStone))
    {
        int Count = 0;

        for (int i = 0; i < 19; i++)
        {
            int NextX = _X + i;

            if (NextX >= 19)
            {
                break;
            }

            if (_Board[_Y][NextX] == CurStone)
            {
                Count++;
            }
            else
            {
                break;
            }
        }

        if (Count == 5)
        {
            return true;
        }
    }

    //우하
    if (!(_X - 1 >= 0 && _Y - 1 >= 0 && _Board[_Y - 1][_X - 1] == CurStone))
    {
        int Count = 0;

        for (int i = 0; i < 19; i++)
        {
            int NextX = _X + i;
            int NextY = _Y + i;

            if (NextX >= 19 || NextY >= 19)
            {
                break;
            }

            if (_Board[NextY][NextX] == CurStone)
            {
                Count++;
            }
            else
            {
                break;
            }
        }

        if (Count == 5)
        {
            return true;
        }
    }

    //하
    if (!(_Y - 1 >= 0 && _Board[_Y - 1][_X] == CurStone))
    {
        int Count = 0;

        for (int i = 0; i < 19; i++)
        {
            int NextY = _Y + i;

            if (NextY >= 19)
            {
                break;
            }

            if (_Board[NextY][_X] == CurStone)
            {
                Count++;
            }
            else
            {
                break;
            }
        }

        if (Count == 5)
        {
            return true;
        }
    }

    return false;
}

Check함수 내부이다.

무식하게 4방향에 대해 모드 반복문을 돌아주었다.

코드 전문

#include <iostream>
#include <vector>

void Init()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
}

bool Check(const std::vector<std::vector<int>>& _Board, int _X, int _Y)
{
    int CurStone = _Board[_Y][_X];

    //우상
    if (!(_X - 1 >= 0 && _Y + 1 < 19 && _Board[_Y + 1][_X - 1] == CurStone))
    {
        int Count = 0;

        for (int i = 0; i < 19; i++)
        {
            int NextX = _X + i;
            int NextY = _Y - i;

            if (NextX >= 19 || NextY < 0)
            {
                break;
            }

            if (_Board[NextY][NextX] == CurStone)
            {
                Count++;
            }
            else
            {
                break;
            }
        }

        if (Count == 5)
        {
            return true;
        }
    }

    //우
    if (!(_X - 1 >= 0 && _Board[_Y][_X - 1] == CurStone))
    {
        int Count = 0;

        for (int i = 0; i < 19; i++)
        {
            int NextX = _X + i;

            if (NextX >= 19)
            {
                break;
            }

            if (_Board[_Y][NextX] == CurStone)
            {
                Count++;
            }
            else
            {
                break;
            }
        }

        if (Count == 5)
        {
        return true;
        }
    }

    //우하
    if (!(_X - 1 >= 0 && _Y - 1 >= 0 && _Board[_Y - 1][_X - 1] == CurStone))
    {
        int Count = 0;

        for (int i = 0; i < 19; i++)
        {
            int NextX = _X + i;
            int NextY = _Y + i;

            if (NextX >= 19 || NextY >= 19)
            {
                break;
            }

            if (_Board[NextY][NextX] == CurStone)
            {
                Count++;
            }
            else
            {
                break;
            }
        }

        if (Count == 5)
        {
            return true;
        }
    }

    //하
    if (!(_Y - 1 >= 0 && _Board[_Y - 1][_X] == CurStone))
    {
        int Count = 0;

        for (int i = 0; i < 19; i++)
        {
            int NextY = _Y + i;

            if (NextY >= 19)
            {
                break;
            }

            if (_Board[NextY][_X] == CurStone)
            {
                Count++;
            }
            else
            {
                break;
            }
        }

        if (Count == 5)
        {
            return true;
        }
    }

    return false;
}

int main()
{
    Init();

    std::vector<std::vector<int>> Board(19, std::vector<int>(19, 0));
    for (int i = 0; i < 19; i++)
    {
        for (int j = 0; j < 19; j++)
        {
            std::cin >> Board[i][j];
        }
    }

    for (int i = 0; i < 19; i++)
    {
        for (int j = 0; j < 19; j++)
        {
            if (Board[i][j] == 0)
            {
                continue;
            }

            if (Check(Board, j, i) == true)
            {
                std::cout << Board[i][j] << "\n";
                std::cout << i + 1 << " " << j + 1;

                return 0;
            }
        }
    }

    std::cout << 0;

    return 0;
}

컴퓨터 렌더링 최적화에 관한 정보를 찾으면, '드로우 콜'이라는 용어를 시도 때도 없이 만나게 될 것이다.

드로우 콜이라는 것은 CPU 병목의 주 원인으로 꼽히며, 게임 최적화에서 빼놓을 수 없는 존재이다.

드로우 콜에 대해 알아보자.

드로우 콜

먼저, 드로우 콜이라는 것은 간단하게 말하자면, CPU가 GPU에게 렌더링을 명령하는 것이다.

DirectX, Open GL, Vulkan 같은 그래픽스 API를 사용해서 게임을 만들게 되면, 렌더링을 할 때 그래픽카드의 도움을 받아서 연산을 진행하게 된다. DirectX의 경우 그래픽카드의 연산을 활용하기 위해, DeviceContext에 쉐이더도 세팅하고 렌더타겟도 세팅하고 뷰포트토 세팅하고 많은 세팅을 하게 된다. 그렇게 그래픽카드에 여러 명령을 보내서 렌더링을 실행하게 된다. 

드로우 콜의 과정을 알아보자.

먼저, 우리는 API에서 제공해주는 기능을 토대로 버퍼와 쉐이더를 생성하게 된다. 그 과정에서, GPU의 메모리에 해당 정보가 저장되게 된다. 버텍스 버퍼, 인덱스 버퍼, 픽셀 쉐이더, 뎁스 스텐실 등의 모든 정보가 GPU메모리 상에 저장되는 것이다.

GPU는 이 정보들과 RenderState를 기준으로 렌더링을 진행하게 된다. 

RenderState란?

: 어떤 대상을 어떻게 그릴지에 대한 정보를 저장하고 있는 테이블.

예를 들어, A라는 캐릭터를 툰 쉐이더를 이용해 그리고자 한다고 해보자. 그렇다면, A의 버텍스 버퍼, 인덱스 버퍼, 사용할 텍스쳐, 사용할 버텍스 쉐이더, 픽셀 쉐이더, 알파블렌딩, 뎁스 스텐실 등등 수많은 정보가 필요하다.

이미 모든 정보는 GPU의 메모리에 저장되어 있지만, 지금 어떤 것을 이용해 그릴 지는 알 수가 없다.

그 것에 대한 정보를 저장하고 있는 것이 RenderState이다.

위의 그림처럼, 현재 렌더링을 실행할 때 어떤 것을 사용하여 렌더링을 할 지에 대한 정보를 담고 있는 것이 Render State이며, Render State의 각 값은 GPU 메모리의 주소값으로 보유하고 있게 된다.

그렇다면, Render State에서 현재 어떤 것을 가지고 렌더링을 실행할 것인가는 어떻게 정해지는 것일까?
CPU에서 명령을 하게 된다.

위처럼, 렌더링를 하기 전에 우리는 버텍스 버퍼를 세팅하고, 버텍스 쉐이더를 세팅하고, 픽셀 쉐이더를 세팅하는 등 현재 렌더링에서 사용되어야 할 머티리얼을 세팅해준다. 

이러한 함수들이 그래픽카드의 Render State를 바꾸라는 명령인 것이다.

이렇게 Render State를 의도한 대로 모두 변경하고 나면, Direct X에선 Draw함수를 실행하게 된다. (Draw, DrawAuto, DrawIndexed..)

해당 함수는 렌더링 세팅이 완료 되었으니, 이제 그림을 그려라! 라는 명령인 것이다.

이 명령을 DP Call 이라고 한다. (Draw Primitive Call)

DP Call 명령은 즉각적으로 GPU에서 처리하는 것은 아니고, CPU의 Command Buffer에 명령어를 저장해놓으면 GPU에선 명령 처리가 가능할 때, 가장 앞의 명령어를 꺼내서 실행하는 방식이다.

(GPU가 기존 작업을 끝낼 때까지 CPU가 대기할 필요도 없고, GPU도 명령받은 작업들을 효율적으로 처리할 수 있다.)

이처럼, Render State 변경 명렁을 내리고 DP Call을 하는 것을 통틀어 Draw Call이라고 부르는 것이다.

드로우 콜은 기본적으로 CPU에서 GPU로 보내는 명령이기 때문에, 명령을 GPU가 알아듣도록 변환할 필요가 있다. 이 과정에서 아주 많은 오버헤드가 발생한다고 한다.

드로우 콜의 오버헤드를 줄이는 법

많은 사람들이 착각하는 것중 하나가 한 메쉬의 버텍스 개수가 적어지면 드로우 콜의 오버헤드가 완화될 것이라고 기대하는 것이다. 앞에서 말했듯이 버텍스 버퍼는 이미 GPU 메모리에 저장되어 있고, 포인터를 이용해서 Render State를 변경하게 된다.

즉, CPU에서 GPU로 데이터를 보내는 과정은 버텍스의 개수와는 큰 관련이 없고, GPU에서 렌더링 연산을 수행하는 것과 연관이 있는 것이다. 버텍스의 개수는 CPU의 연산 부담을 늘리는 것이 아니라 GPU의 연산 부담을 늘리는 것이다

.드로우 콜의 오버헤드를 줄이기 위해선, 텍스쳐 퀄리티를 낮춘다거나 버텍스의 개수를 낮추는 등의 작업이 필요한 것이 아니라 드로우 콜 자체의 횟수를 줄이는 것이 중요하다.

드로우 콜은 무언가를 그려야 할 때마다 호출하게 된다. 예를 들어, 메쉬 3개로 이루어진 캐릭터는 3번의 드로우콜을 호출해야 하며, 반대로 메쉬가 1개인 캐릭터라도 외곽선 등의 추가적인 효과를 적용하기 위해 2번 이상 드로우 콜을 호출할 수도 있다.

즉, 메쉬의 개수 혹은 머티리얼의 개수에 따라 드로우 콜의 호출 빈도가 결정되는 것이다.

그렇다면, 무작정 매쉬의 수를 줄이거나 머티리얼의 수를 줄여버리면 될까?

물론 아니다. 그래픽 퀄리티를 조금이라도 올리기 위해 하드웨어 성능을 극한까지 사용하는 사람들도 있는 와중에, 매쉬와 머티리얼을 줄여서 퀄리티를 포기한다는 것은 올바른 해결법이 아니다.

그렇다면, 여러 개의 메쉬를 한 번의 드로우 콜로 해결할 수 있다면?
여러 번 그려야 하는 것을 한 번의 드로우 콜로 해결하고자 하는 것이 배칭이다.

배칭

하나의 캐릭터 모델을 눈 메쉬, 머리 메쉬, 상체 메쉬, 하의 메쉬로 쪼개놓았다고 해보자.

그렇다면, 4개의 메쉬는 다른 머티리얼을 쓸까? 물론 그런 상황도 있겠지만, 일반적으로는 모두 같은 머티리얼을 사용해서 렌더링하게 된다. 차이가 있다면, 텍스쳐는 모두 다른 텍스쳐를 사용할 것이다.

즉, 거의 모든 렌더 스테이트가 동일한데 텍스쳐 하나 때문에 4번의 드로우 콜을 보내야 하는 것이다.

하지만, 아틀라스 텍스쳐를 사용한다면?

아틀라스 텍스쳐란, 하나의 이미지 파일에 위처럼 여러 오브젝트에 사용될 텍스쳐를 모아놓은 것이다.

여기서 UV값을 이용하여 필요한 만큼 잘라서 텍스쳐를 메쉬에 입히는 것이다.

이러한 이미지 파일로 텍스쳐를 생성한 뒤, 부위별로 UV만 매칭해준다면 서로 다른 메쉬이지만 같은 텍스쳐를 사용하는 셈이 되는 것이다. 즉, 눈, 머리, 상의, 하체에 대해 렌더 스테이트가 완전히 동일해지는 것이다.

이러한 경우엔 4개의 메쉬를 하나로 합쳐버리더라도 품질의 손상 없이 렌더링이 가능해진다.

(메쉬를 나눠놓는 이유가 대부분 다른 텍스쳐를 입히기 위함이다.)

아틀라스 이미지를 활용하면, 여러 메쉬를 하나로 합치는 것이 가능하고 드로우 콜을 1번으로 압축하는게 가능하게 된다는 것이다!

즉 배칭이란, 같은 머티리얼을 사용하는 여러 메쉬를 하나로 합쳐 한 번의 드로우 콜로 렌더링하는 방식이라는 것이다.

배칭은 스태틱 배칭, 다이나믹 배칭 두 가지 종류가 있다.

스태틱 배칭은 로딩 타임에 미리 매쉬들을 배칭하는 것이다. 주로 움직이지 않는 오브젝트(맵, 장식물등)에 대해 사용한다.

여러 메쉬 중 같은 머티리얼을 사용하는 메쉬를 하나로 묶어, 한 번의 드로우콜로 렌더링을 해결하게 해준다.

다이나믹 배칭은 런타임에 배칭을 진행하는 것이다. 주로 움직이는 대상에 대해 사용한다.

실시간으로 오브젝트를 하나로 합치는 연산을 진행하며, 드로우 콜을 줄인다고 한다.

하지만, 이러한 배칭에도 문제가 있다.

스태틱 배칭의 문제점

1. 메모리 사용량이 증가한다.

: 덩어리로 합친 메쉬를 추가적으로 VRAM (GPU 메모리)에 올려놓아야 하기 때문에 메모리 사용량이 증가한다.

2. 컬링을 제대로 적용할 수 없어진다.

: 메쉬가 나누어져 있을 땐, 화면 밖으로 벗어난 메쉬만 렌더링 하지 않는 것이 가능하지만 하나로 합쳐버리는 순간  화면을 벗어나는 부분만 렌더링 하지 않는 것이 불가능해진다.

다이나믹 배칭의 문제점

1. 연산량이 너무 많다.

: 실시간으로 연산하기엔 연산량이 너무 많아, 버텍스의 수가 많으면 오히려 드로우 콜을 줄임으로써 얻는 이득보다 배칭으로 얻는 손해가 더 커질 수 있다고 한다.

배칭이라는 기술이 여러모로 효율적으로 보이는 것 같으면서도, 상황에 따라 비효율적일 수 있기 때문에 신중하게 사용하는 것이 좋을 것 같다.

 

일반적인 공약수를 구하는 문제를 반대로 제시한 문제이다.

A와 B가 주어졌을 때 GCD와 LCM을 구하는 것이 아니라, GCD와 LCM이 주어졌을 때 A와 B를 구하는 문제이다.

물론, A와 B의 쌍은 여럿 존재할 수 있기 때문에 그 중에서 A와 B의 합이 최소인 쌍을 출력해주면 된다.

문제 풀이

먼저, 두 수 A,B에 최대 공약수를 G, 최소공배수를 L이라고 한다면 A와 B는 반드시 GCD의 배수이다.

이를 이용하여, L보다 작은 G의 배수를 모두 구한 뒤, 그 중 2개를 뽑아 두 수의 최소 공배수와 최대 공약수가  G, L과 동일한지를 검사하여 조건을 만족하는 (A, B)쌍을 모두 구할 수 있을 것이다.

하지만, 문제의 조건을 보면 숫자의 범위가 2~100,000,000이다.

위와 같은 방식으로 답을 구하려고 했다간 시간초과가 발생할 수 밖에 없다.

그렇기 때문에, 위에서 주어진 풀이 방법을 기반으로 범위를 좁히는 것이 필요하다.

두 수를 구하기 위해 과연 G보다 작은 L의 배수를 모두 구해야 할까?

먼저 한 가지 수식을 보자.

$$GCD = \frac{A * B}{LCM}$$

유클리드 호제법에 따르면, 위 공식이 성립한다.

여기서 변환을 하나 해보자.

$$GCD * LCM = A * B$$

이렇게도 표현할 수 있을 것이다.

A와 B의 곱이 GCD * LCM 이라고 한다면, A와 B 둘 중 하나는 반드시 GCD * LCM의 제곱근보다 작거나 같아야 한다.

즉, LCM보다 작은 GCD의 배수를 모두 구하는 것이 아니라, GCD * LCM의 제곱근보다 작은 GCD의 배수에서만 값을 구하면 된다.

또한, GCD * LCD = A * B 이므로, A를 결정하였다면, GCD * LCD를 A로 나눠서 바로 B를 구할 수도 있기 때문에, GCD의 배수를 모두 구할 필요가 없게 된다.

풀이 코드

long long GCD = 0;
long long LCM = 0;

std::cin >> GCD >> LCM;

GCD와 LCM을 입력받았다.

long long Mul = GCD * LCM;
long long MulSqrt = std::sqrt(Mul);

두 수의 곱의 제곱근도 구해주었다.

long long MinSum = LLONG_MAX;
std::pair<int, int> Answer;

for (int i = GCD; i <= MulSqrt; i += GCD)
{
    long long  Cur = i;
    long long  Other = Mul / Cur;

    int  CurGCD = GetGCD(Cur, Other);
    long long  CurLCM = Cur * Other / CurGCD;

    if (CurGCD == GCD && CurLCM == LCM)
    {
        if (Cur + Other < MinSum)
        {
            MinSum = Cur + Other;
            Answer = { Cur, Other };
        }
    }
}

이후, 반복문을 돌며 위에서 말한 논리로 두 숫자 쌍을 구해주었다.

GCD의 배수에 대해서만 검사를 하도록 하였으며, 숫자 1개를 구했다면 GCD * LCM을 해당 숫자로 나누어 다른 숫자도 구해주었다.

그리고 두 숫자의 최소 공배수와 최대 공약수가 입력받은 값과 동일한지를 검사하여 조건을 만족하는 두 숫자인지 검사한 뒤, 두 수의 합을 기준으로 Answer를 갱신해주었다.

long long GetGCD(int _Left, int _Right)
{
	int Remain = _Left % _Right;

	while (Remain > 0)
	{
		Remain = _Left % _Right;
		_Left = _Right;
		_Right = Remain;
	}

	return _Left;
}

최대 공약수는 위와 같이 유클리드 호제법으로 구해주었다.

std::cout << Answer.first << " " << Answer.second;

return 0;

마지막에 답을 출력해주면 끝이다.

코드 전문

#include <iostream>
#include <algorithm>
#include <vector>
#include <climits>
#include <cmath>

void Init()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
}

long long GetGCD(int _Left, int _Right)
{
    int Remain = _Left % _Right;

    while (Remain > 0)
    {
        Remain = _Left % _Right;
        _Left = _Right;
        _Right = Remain;
    }

    return _Left;
}

int main()
{
    Init();

    long long GCD = 0;
    long long LCM = 0;

    std::cin >> GCD >> LCM;

    long long Mul = GCD * LCM;
    long long MulSqrt = std::sqrt(Mul);

    long long MinSum = LLONG_MAX;
    std::pair<int, int> Answer;

    for (int i = GCD; i <= MulSqrt; i += GCD)
    {
        long long  Cur = i;
        long long  Other = Mul / Cur;

        int  CurGCD = GetGCD(Cur, Other);
        long long  CurLCM = Cur * Other / CurGCD;

        if (CurGCD == GCD && CurLCM == LCM)
        {
            if (Cur + Other < MinSum)
            {
                MinSum = Cur + Other;
                Answer = { Cur, Other };
            }
        }
    }

    std::cout << Answer.first << " " << Answer.second;
    	
    return 0;
}

 

문제 이해가 처음에 다소 헷갈리는 부분이 있었다.

먼저, Defile 프로젝트는 위의 설명과 같다.

모든 국회의원의 명예를 1씩 감소시키고, 0이 된 국회의원이 있다면 해당 국회의원을 파면한다.

이 과정을 반복하며 모든 국회의원을 박탈하는 것이 목표이다.

다만, 해커를 이용한 명예 실추가 본인은 Defile프로젝트의 1번 과정과 관련이 있는 건가 싶었는데, 이는 일종의 사전작업이라고 생각하면 될 듯하다.

경우에 따라 Defile 프로젝트를 실행하더라도, 모든 국회의원을 파면할 수 없을 수도 있다. 이런 상황을 방지하기 위해, 해커를 이용해 명예를 미리 감소시켜놓는 것이다.

즉, Defile 프로젝트를 성공시키기 위해 해커를 이용해 사전 작업을 한다고 가정했을 때, 해커를 최소 몇 명을 고용해야 하는가? 를 구하는 문제이다.

문제 풀이

먼저, Defile프로젝트를 성공시키기 위한 조건을 생각해보자.

조건을 보면, 모든 국회의원의 명예를 1씩 실추시킨 뒤, 파면되는 국회의원이 없다면 해당 프로젝트는 종료된다.

즉, 첫 시도에서 적어도 1명 이상의 국회의원이 파면되어야 한다는 것이다.

=> 명예가 1인 국회의원이 적어도 1명 있어야 한다.

또한, 첫 번째 시도만 성공해야 하는 것이 아니라 매 시도마다 파면되는 국회의원이 반드시 1명은 있어야 한다.

(1명도 없는 순간에는 프로젝트가 종료되기 때문에)

생각해보면, 모든 국회의원의 명예를 1씩 실추하게 되면, 1인 국회의원은 명예가 0이 되므로 파면될 것이다.

그렇다면 그 다음 시도에서 파면될 국회의원은? 1이 실추된 이후에 남은 명예가 1인 국회의원일 것이다.

즉, 처음 명예가 2인 국회의원이 두 번째 시도에서 파면될 것이다.

이 논리를 반복적으로 이어가보면, 명예가 1인 국회의원이 처음 파면되고 그 다음엔 명예가 2인 국회의원이 파면되며 그 다음엔 명예가 3인 국회의원이 파면되고 이 과정이 반복될 것이다.

즉, 모든 국회의원을 명예 순으로 정렬했을 때 이전 국회의원의 명예와 2이상 차이가 나는 국회의원이 없어야 한다는 것이다.

(한 국회의원을 파면한 이후에 파면되는 국회의원은 파면된 국회의원의 명예보다 1만큼 큰 명예를 가진 국회의원이므로)

그러므로, 해커를 이용해 맞추어야할 사전 작업은 아래와 같다.

1. 모든 국회의원중 1의 명예를 가진 국회의원이 적어도 1명 존재해야 한다.

2. 모든 국회의원을 명예 기준으로 오름차순 정렬했을 때, 어떤 국회의원의 명예가 앞의 국회의원과 2이상 차이가 나서는 안된다.

하나의 예시를 보자.

7 3 6 2 4

국회의원의 명예가 위와 같이 입력되었다고 해보자.

이를 오름차순으로 정렬하면, 2 3 4 6 7 이 된다.

반드시, 명예가 1인 국회의원이 1명은 존재해야 하므로 해커를 이용해 맨 앞의 국회의원의 명예를 1을 실추시켜야 한다.

-> Hacker 1명 고용 

-> 명예 : 2 3 4 6 7 -> 1 3 4 6 7 로 변경

모든 국회의원은 앞의 국회의원의 명예보다 2이상 큰 명예를 지녀선 안된다.

두 번째 국회의원부터 명예를 실추해보자.

첫 번째 국회의원의 명예가 1이므로, 두 번째 국회의원의 명예는 최대 2까지 보유할 수 있다.

->Hacker 1명 고용

-> 명예 : 2 3 4 6 7 -> 1 2 4 6 7 로 변경

두 번째 국회의원의 명예가 2이므로 세번째 국회의원의 명예는 최대 3까지 보유할 수 있다.

->Hacker 1명 고용

-> 명예 : 1 2 4 6 7 -> 1 2 3 6 7 로 변경

세 번째 국회의원의 명예가 3이므로 네 번째 국회의원의 명예는 최대 4까지 보유할 수 있다.

->Hacker 2명 고용

-> 명예 : 1 2 3 6 7 -> 1 2 3 4 7 로 변경

네 번째 국회의원의 명예가 4이므로 다섯 번째 국회의원의 명예는 최대 5까지 보유할 수 있다.

->Hacker 2명 고용

-> 명예 : 1 2 3 6 7 -> 1 2 3 4 5 로 변경

총 7명의 해커를 고용하여 모든 조건은 만족시키도록 하였다.

이 상태에서 defile 프로젝트를 실행하게 되면 아래와 같은 과정을 거치며 모든 국회의원의 명예를 실추할 수 있다.

첫 명예 : 1 2 3 4 5

1번째 시도 : 0 1 2 3 4

2번째 시도 : 0 0 1 2 3

3번째 시도 : 0 0 0 1 2

4번째 시도 : 0 0 0 0 1

5번째 시도 : 0 0 0 0 0

이처럼 7명의 해커를 이용해 미리 명예를 실추해놓으면, 1번의 Defile 프로젝트를 통해 모든 국회의원을 파면할 수 있다.

코드 풀이

int NumOfMan = 0;
std::cin >> NumOfMan;

std::vector<int> Honors(NumOfMan, 0);
for (int i = 0; i < NumOfMan; i++)
{
    std::cin >> Honors[i];
}

먼저, 국회의원의 수와 명예를 입력받는다.

std::sort(Honors.begin(), Honors.end());

이후, 명예를 오름차순으로 정렬한다.

long long HackerCount = Honors[0] - 1;
Honors[0] = 1;

해커를 고용하여 가장 작은 명예를 1로 맞춰준다.

참고로, 국회의원은 최대 10만명이고 명예는 최대 10만이므로 HackerCount의 최대값은 int범위를 초과한다.

그러므로 long long 자료형으로 선언해주어야한다.

for (int i = 1; i < NumOfMan; i++)
{
    int CurHonor = Honors[i - 1] + 1;

    if (Honors[i] > CurHonor)
    {
        int Gap = Honors[i] - CurHonor;
        HackerCount += Gap;
        Honors[i] = CurHonor;
    }
}

반복문을 돌며, 이전 인덱스의 명예보다 2 이상 차이나지 않도록 갱신해주었다.

그 과정에서 명예를 깎는 만큼 HackerCount를 증가시켜주었다.

std::cout << HackerCount;

return 0;

마지막으로 HackerCount를 출력해주면 끝이다.

코드 전문

#include <iostream>
#include <vector>
#include <algorithm>

void Init()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
}

int main()
{
    Init();

    int NumOfMan = 0;
    std::cin >> NumOfMan;

    std::vector<int> Honors(NumOfMan, 0);
    for (int i = 0; i < NumOfMan; i++)
    {
        std::cin >> Honors[i];
    }

    std::sort(Honors.begin(), Honors.end());

    long long HackerCount = Honors[0] - 1;
    Honors[0] = 1;

    for (int i = 1; i < NumOfMan; i++)
    {
        int CurHonor = Honors[i - 1] + 1;
        
        if (Honors[i] > CurHonor)
        {
            int Gap = Honors[i] - CurHonor;
            HackerCount += Gap;
            Honors[i] = CurHonor;
        }
    }

    std::cout << HackerCount;

    return 0;
}

 

dobarz

adatak 

두 개의 문자열이 입력되었다고 치자.

이 때, 각 열을 준으로 문자열을 새로 만들게 되면, "da", "od", "ba", "at", "ra", "zk" 총 6개의 문자열이 만들어진다.

첫 번째 행의 문자열을 제거한 뒤, 동일한 방법으로 문자열을 만들게 되면, "a", "d", "a", "t", "a", "k" 총 6개의 문자열이 만들어진다.

처음에 만들었던 "da", "od", "ba", "at", "ra", "zk" 간에는 중복이 존재하지 않는다.

두 번째로 만든  "a", "d", "a", "t", "a", "k" 에는 "a"가 총 3번 중복되고 있다. 

즉, 기존의 문자열을 1개 제거했더니 열 문자열에서 중복되는 문자열이 발생한 것이다.

이처럼, 입력으로 주어진 문자열에서 몇 개를 지우면 열 문자열에서 중복되는 문자열이 발생하는지를 구하면 된다.

위의 예시에선 1을 답으로 출력하면 된다.

문제 풀이

아주 단순하게 접근하였다.

주어진 문자열을 기반으로 열 문자열을 만들어서 자료구조에 저장한 뒤, 맨 앞의 문자를 하나씩 지워가며 중복 검사를 진행한 것이다.

하지만, 문자열의 경우 맨 앞의 문자를 제거하면 뒤의 모든 문자를 앞으로 땡겨오는 연산을 해야하는 문제가 있다.

그러므로, 열 문자열을 저장할 때 앞뒤를 뒤집은 상태로 저장하고 맨 뒤의 문자를 제거하면서 중복 검사를 하였다.

중복검사는 unordered_set을 이용해서 하였다. unordered_set에 모든 문자열을 삽입한 뒤, 문자의 개수와 unordered_set의 size가 동일한지를 테스트하여 중복 여부를 검사하였다.

풀이 코드

int StrSize = 0;
int VecSize = 0;
std::cin >> StrSize >> VecSize;

std::vector<std::string> Vec(VecSize, std::string(StrSize, '0'));
for (int i = 0; i < StrSize; i++)
{
    for (int j = 0; j < VecSize; j++)
    {
        std::cin >> Vec[j][StrSize - 1 - i];
    }
}

벡터에 열 문자열을 모두 저장해주고 있다.

앞에서 말했던 것처럼, 열 문자열을 저장할 때 뒤집어서 저장을 해주고 있다.

int Count = 0;

for(int j = 0; j < StrSize; j++)
{
    for (int i = 0; i < VecSize; i++)
    {
        Vec[i].pop_back();
    }

    std::unordered_set<std::string> Strs;

    for (int i = 0; i < VecSize; i++)
    {
        Strs.insert(Vec[i]);
    }

    if (Strs.size() == VecSize)
    {
        Count++;
    }
    else
    {
        break;
    }
}

이후, 모든 문자열의 가장 마지막 원소(실제로는 열 문자열의 가장 앞 문자)를 제거해주었다.

그리고 unordered_set에 모든 문자열을 삽입하였고, unordered_set의 size와 기존 문자열의 개수와 동일한지를 검사하여 Count를 증가시키거나 반복문을 탈출하도록 분기를 두었다.

std::cout << Count;

return 0;

반복문이 끝나고 Count를 출력하면 끝이다.

코드 전문

#include <iostream>
#include <vector>
#include <unordered_set>

void Init()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
}

int main()
{
    Init();

    int StrSize = 0;
    int VecSize = 0;
    std::cin >> StrSize >> VecSize;

    std::vector<std::string> Vec(VecSize, std::string(StrSize, '0'));
    for (int i = 0; i < StrSize; i++)
    {
        for (int j = 0; j < VecSize; j++)
        {
            std::cin >> Vec[j][StrSize - 1 - i];
        }
    }

    int Count = 0;
    
    for(int j = 0; j < StrSize; j++)
    {
        for (int i = 0; i < VecSize; i++)
        {
            Vec[i].pop_back();
        }

        std::unordered_set<std::string> Strs;

        for (int i = 0; i < VecSize; i++)
        {
            Strs.insert(Vec[i]);
        }

        if (Strs.size() == VecSize)
        {
            Count++;
        }
        else
        {
            break;
        }
    }

    std::cout << Count;

    return 0;
}

본인은 현재 8GB의 DRAM을 2개 장착하여 사용하고 있다.

총 16GB의 메인메모리 용량이 확보된 것이다.

언리얼 엔진을 켜고 게임을 만들다 보면 이게 16GB안에 다 들어간다고? 싶을 때가 많다.

언리얼 엔진 하나만 해도 메모리 사용량이 엄청난데, 그 와중에 게임도 구동을 해야한다. 심지어 본인은 노래를 켜고 인터넷 검색을 하거나 동영상을 틀어놓고 하기도 한다. 어쩔 땐, 예제 프로젝트를 참고하기 위해 2~3개의 언리얼 엔진 프로젝트를 켜고 작업하기도 한다. 

상식적으로 생각했을 땐, 16GB라는 메모리의 용량은 턱없이 부족할 것 같다는 생각이 들었다. 물론, 실제로도 부족하다.

부족한데 어떻게 그 모든 프로그램들을 실행하고 감당할 수 있는 것일까?

이는 가상메모리라는 기술 덕분이다.

가상 메모리

가상 메모리의 아이디어는 이렇다. 

4GB짜리 프로세스를 메모리에 올리더라도, 한 번에 사용되는 공간은 4GB가 되지 않을텐데 그러면 사용되고 있는 만큼만 메모리에 나누어서 올리면 되지 않을까? 

프로세스가 전체적으로 필요한 용량은 4GB라고 하더라도, 동시에 4G가 모두 사용되지는 않는다. 그러므로 지금 당장 사용되는 만큼만 메모리에 적재하고 나머지는 적재하지 말자는 개념으로 시작된 것이 가상 메모리이다.

하지만 프로세스는 실행되는 순간부터 모든 정보가 어딘가에는 저장이 되어 있어야 한다. 메모리에 저장을 안할거면 어디다가 할까?

바로 보조 기억 장치이다. HDD, SDD와 같은 저장 장치의 도움을 받아 가상 메모리를 구현하게 된다.

모든 정보를 일단 보조 기억 장치에 적재해둔 뒤, 지금 당장 필요한 부분만 꺼내서 메인 메모리에 적재하고 사용되지 않게 되면 다시 보조 기억 장치로 적재하는 방식인 것이다.

그렇다면, 어떤 방식으로 보조 기억 장치와 메모리 사이에서 정보를 옮기는 것일까?

가상 메모리를 실현하는 방법은 페이징, 세그멘테이션 2가지의 기법이 있다.

페이징

먼저 프로세스와 메인 메모리를 동일한 크기로 조각을 낸다.

예를 들어, 1byte로 쪼갠다고 한다면, 하나의 페이지는  하나의 프레임에 저장될 수 있을 것이다.

프로세스의 페이지는 각 프로세스마다 0번부터 시작하여 인덱스가 매겨진다.

반면, 메인 메모리는 하나이기 때문에 0번 페이지가 0번 프레임에 매칭되는 것은 아니다.

페이지는 메인 메모리의 어느 프레임으로 매칭이 될 것이며, 해당 정보는 운영 체제가 보유한 페이지 테이블에 저장이 된다.

프로세스 A가 실행되면서, 0번 페이지에 있는 정보와 4번 페이지에 있는 정보다 지금 필요하다고 해보자.

그렇다면, 메인 메모리의 어느 프레임에 0번 페이지와 4번 페이지의 데이터를 적재하게 될 것이다.

위에서 말했듯이, 페이지의 인덱스와 프레임의 번호는 항상 일치하는 것이 아니다. (오히려 일치하지 않는 상황이 더더욱 많다.)

그렇기 때문에, 어떤 프레임에 어떤 페이지가 적재되어 있는지 정보를 저장할 곳이 필요하다.

이 것이 운영 체제가 보유한 페이지 테이블이다.

하지만, 이렇게 쪼개져있고 위치도 계속 왔다갔다 하는 상황이라면, CPU에선 무엇을 기준으로 주소를 인식해야 할까?

프로세스의 시작점을 기준으로 가상주소를 부여하는 것이다.

예를 들어, 메인 메모리의 주소와 동일한 개념으로 보았을 때 페이지 하나에 10개의 주소가 포함되어 있다고 해보자.

그렇다면, 페이지 0에는 0~9번지가 있으며, 페이지 1에는 10~19번지가 있고, 페이지 2에는 20~29번지가 있다고 할 수 있을 것이다.

이처럼 하나의 프로세스의 시작을 0번으로 해서, 주소를 생성해준다. 이렇게 만든 주소가 가상 주소이다.

실제로 메인 메모리에 적재되면, 가상 주소와는 다른 물리 주소를 보유하게 된다. (실제 메모리의 주소)

CPU에선 해당 가상 주소를 기준으로 작업을 처리하게 된다. 예를 들어, 가상주소가 5번지인 데이터가 있다면 메인 메모리의 몇 번지에 적재되어 있든간에 5번지의 데이터를 요구하는 것이다.

가상 주소를 특정 방법을 통 물리주소로 변환하고, 메인메모리에선 해당 물리 주소의 데이터를 CPU에 전달하게 된다.

하지만, 페이징 기법에는 몇 가지 단점이 존재한다.

1. 마지막 페이지에서 내부 단편화가 발생

하나의 프로세스를 동일한 크기로 쪼개는 과정을 거치는 페이징은 프로세스의 크기가 페이지 1개 크기의 배수가 아니라면, 프로세스의 마지막 페이지는 페이지의 크기를 전부 채우지 못한다.

예를 들어, 한 페이지가 10byte라고 가정하고 프로세스 A는 91Byte라고 해보자. 마지막 페이지에선 1Byte만 사용하게 되고, 9Byte만큼의 내부 단편화가 발생하게 된다.

2. 페이지 테이블 크기만큼의 메모리를 추가로 소모해야 함

프로세스의 크기가 클수록, 페이지의 크기가 작을수록 페이지 테이블의 크기는 더욱 커질 것이다. 페이지 테이블은 메인 메모리에 항상 적재되어 있기 때문에 페이지 테이블 크기 만큼의 메모리 공간을 활용할 수 없게 된다.

3. 메모리에 두 번 접근해야 함

메모리에 접근하는 시간은 CPU를 기준으로 보았을 때 매우 느린 시간이다. 이를 커버하기 위해 캐시라는 저장 장치를 활용할 정도로 CPU입장에선 메모리에 최대한 직접 접근하지 않는 것이 좋다. 하지만, 페이징 기법의 경우엔 페이지 테이블에 한 번 접근하여 물리적 주소를 알아낸 후, 실제 물리적 주소에 접근하는 두 번의 과정을 거쳐야 한다. 이는 상당한 오버헤드로 다가올 수 있다.

하지만, 실제로는 이를 해결하기 위해 TLB라는 버퍼를 사용하고 있다. 물론, 문제를 완전히 해결하는 것은 아니고 CPU의 캐시와 동일하게 최근에 사용된 페이지 테이블의 데이터를 가져와서 빠르게 탐색하는 용도로 사용한다. 캐시 미스 발생시 메모리에서 데이터를 다시 복사하는 것처럼, TLB또한 TLB 미스 발생시 메모리에 다시 접근하여 데이터를 가져오는 방식으로 사용된다.

세그멘테이션

세그멘테이션은 페이징과 유사하지만 다른 기법이다.

세그멘테이션 또한 프로세스를 여러개의 조각으로 쪼개는 것은 똑같다. 

하지만, 단순히 동일한 크기로 쪼개는 것이 아니라 논리적 특성을 기준으로 프로세스를 쪼개게 된다. 

예를 들어, 우리가 잘 아는 code, data, heap, stack 또한 일종의 세그멘테이션 기법으로 쪼개진 것이다.

데이터들의 용도나 목적을 기준으로 프로세스를 4개의 조각으로 쪼갠 것이다.

이 외에도 지역변수, 전역변수, 함수, 심볼 등을 기준으로 쪼개기도 한다고 한다.

페이징 기법은 페이지와 프레임의 크기가 동일하기 때문에, 페이지를 그대로 메인 메모리의 프레임에 적재하면 됐지만 세그멘테이션의 경우엔 각 세그먼트의 크기가 고정되어 있지 않기 때문에 메인 메모리를 미리 쪼개놓는 것이 불가능하다.

이러한 이유 때문에 세그멘테이션 기법은 그때 그때 각 세그먼트의 크기만큼 메모리 공간을 할당하게 된다. 

세그멘테이션 또한 페이징 테이블처럼 세그먼트 테이블이 존재한다. 하지만, 조각의 수가 적은만큼 차지하는 용량이 매우 작아서 메인 메모리가 아닌 CPU의 레지스터에 저장된다고 한다. 이로 인해, 주소를 찾을 때 메인 메모리에 단 1번만 접근해도 된다.

세그먼트 테이블은 base와 Limit을 저장한다. A라는 세그먼트가 크기가 1400이라고 해보자. A를 메인 메모리의 1000번지로부터 1400 크기만큼 할당하였다면,  base는 1000이 되고 Limit은 1400이 된다.

세그멘테이션이 언뜻 보면 페이징보다 좋아보이지만 실제론 페이징보다 많이 사용되지 않는다.

이유는 하나의 치명적인 문제점 때문이다.

1. 세그멘테이션 기법은 외부 단편화를 야기한다.

세그멘테이션 기법은 위에서 말했듯이, 필요할 때마다 그 크기만큼 메인 메모리 상에 새로 할당하게 된다. 가변적인 크기로 메모리 상에서 할당과 해제를 반복하다 보면 자연스럽게 외부 단편화가 발생할 수 밖에 없다. 이로 인해 세그멘테이션 기법을 사용시에 메모리가 아주 비효율적으로 사용되는 상황이 잦아, 세그멘테이션 기법을 단독으로 사용하는 것은 선호되지 않는다고 한다.

프로그래밍에선 사용가능한 자원을 최대한 효율적으로 활용하는 것이 매우 중요하다.

하지만, 효율적이지 않게 사용되는 상황은 언제든 발생할 수 있다.

대표적으로 메모리가 비효율적으로 사용되는 상황인 내부 단편화와 외부 단편화에 대해 알아보자.

메모리 내부 단편화

위의 그림을 보자. 전체 할당받은 메모리는 회색 네모칸 만큼이다.

하지만, 정작 실제로 사용하고 있는 것은 주황색 네모칸 만큼밖에 되지 않는다.

이 상황에선, 비어있는 회색 네모칸 만큼 메모리가 낭비되고 있다고 할 수 있다. 

이처럼, 실제로 필요한 것보다 더 많은 메모리를 할당하여 메모리가 낭비되는 상황을 내부 단편화라고 한다.

대표적인 예시를 하나 들어보자.

팝업 스토어를 열었다고 가정해보자. 팝업 스토어에 참가하는 손님을 기록하기 위한 장부로 std::vector를 선언하였다.

손님은 64명정도 올 것으로 예상되었고, 그에 맞게 vector를 64만큼 reserve해주었다.

하지만, 실제로 방문한 손님은 32명밖에 되지 않았다. 벡터에 손님 정보를 모두 기록하여도 할당한 메모리의 절반밖에 사용하지 않는 상황이 되어버린 것이다. 현재 32칸의 메모리가 낭비되고 있고, 내부 단편화가 발생하였다고 할 수 있다.

메모리 외부 단편화

이렇게 총 10바이트의 메모리 공간이 있고, 위와 같이 할당이 되어있다고 해보자.

여기서, B와 D의 메모리를 할당 해제할 것이다.

이렇게, B와 D가 있던 공간은 비어있는 공간이 될 것이다.

이때, 4byte짜리 E에 대한 메모리를 할당하려고 한다면?

할당할 수가 없다. 분명 메모리 영역에는 2byte짜리 비어있는 공간이 2개 있으므로 총 4byte가 존재함에도 불구하고, E가 사용할 메모리를 할당할 수가 없다. 왜냐하면, 하나의 데이터는 메모리상에 연속적으로 저장되어야 하기 때문이다. 4byte짜리를 반씩 쪼개서 다른 곳에 저장할 수가 없다는 것이다.

이처럼, 메모리의 용량으로 봤을 땐 충분한 공간이 있음에도 불구하고 메모리를 할당하지 못하거나 효율적으로 사용하지 못하는 상황을 외부 단편화라고 한다.

이러한, 단편화 현상들을 해결하기 위해선 페이징, 세그멘테이션 등 여러 기법을 사용하곤 한다.

이는 다른 게시물에서 상세하게 설명하도록 하겠다.

프로그래밍에서 빼놓을 수 없는 키워드가 스레드와 프로세스이다.

각각의 차이점을 알아보자.

개념

프로세스란?

프로세스는 운영체제에서 자원을 할당받는 작업의 단위이다.
어떠한 프로그램이 실행되어 메모리 상에 올라가게 되면, 그 것을 프로세스라고 한다

스레드란?

스레드란 프로세스 내에서 실행하는 작업의 단위이다.
프로세스가 운영체제로부터 할당받은 자원을 실질적으로 이용하는 주체이다.

예시

편의점을 차려서 돈을 벌고자 하는 목적이 있다고 해보자. 그렇다면, 해당 목적을 위해 많은 설계를 해야 할 것이다. 자본 관리부터, 운영 계획을 설계 및 수립할 것이고, 구체적으로는 진열이나 청소, 손님 응대 등에 관한 것도 설계해야 할 것이다. 이러한 모든 설계 계획을 담고 있는 것이 프로그램이다.

그리고, 모든 계획을 마친 뒤 편의점을 실제로 차리는 순간이 왔다고 해보자. 이 때부터 해당 계획은 프로세스가 된다.해당 계획을 실행하기 위해선 먼저 편의점을 운영할 건물이 있어야 한다. 해당 건물을 운영체제로부터 할당받는 자원이라고 생각하면 된다. 편의점을 운영하기 위해선 건물이라는 물리적 공간이 반드시 필요한 것처럼, 프로세스를 실행하기 위해선 물리적인 메모리 공간을 할당받아야 한다.

편의점을 운영하기 시작했다면, 우리가 계획한 것들을 하나씩 실행해야 한다. 계획은 조금씩 쪼갤 수 있을 것이다.

돈을 번다 -> 물건을 판다 -> 물건을 진열한다.

이런 방식으로 작업을 세분화 했다고 해보자.그렇다면, 돈을 벌기 위해선 일단 물건을 진열하는 일을 해야 한다는 것이다.

물건을 진열하는 일처럼 목적을 위해 실행해야 하는 작은 작업들을 실제로 처리하는 주체를 스레드라고 생각하면 된다. (스레드 = 알바생)

게임을 예로 들어본다면, E키를 누르면 총알을 발사하는 과정을 거치기 위해선 키보드의 키 입력을 감지한 뒤, 해당 키 입력이 E와 같은지 확인하고, 투사체를 생성하고, 위치를 이동시킨 뒤, 화면에 렌더링하는 등의 수많은 작은 작업들을 실행해야 한다.이 작은 작업들 하나하나를 실행하는 주체가 스레드인 것이다.

프로세스는 하나의 거대한 목적이며, 스레드는 그 목적을 이루기 위해 세분화된 작업을 실행하는 주체이다.

구체적인 차이

위와 같은 개념의 차이로부터 발생하는 차이점들이 존재한다.

메모리 영역의 차이

이처럼 여러개 개의 프로세스가 동시에 실행된다면, 각 프로세스는 별도의 메모리 영역을 보유하게 된다.

각 영역은 Code, Data, Heap, Stack으로 분류되며 각각의 프로세스는 다른 프로세스의 메모리 영역을 함부로 침범할 수 없다. 프로세스의 영역이 철저히 구분되어 있는 것이다.

반면, 스레드의 경우 Code, Data, Heap 영역을 프로세스 내의 모든 스레드가 공유한다. 각 스레드는 연산을 하기 위해 각각 stack 영역만 할당받을 뿐, Code,Data,Heap에 대해서는 독립적인 영역을 보유하고 있지 않은 것이다.

이 메모리 영역의 차이로 인해 파생되는 차이점들이 많다.

컨텍스트 스위칭 비용

컨텍스트 스위칭이란 CPU에서 실행중인 작업을 변경하는 과정을 의미한다. 프로세스 A를 실행하고 있다가 프로세스 B를 실행하기 위해선, CPU의 레지스터 저장되어 있는 프로세스 A 관련 데이터를 모두 별도의 공간에 저장해놓은 뒤, 프로세스 B와 관련된 데이터를 새로 올려야 한다. 프로세스 단위로 작업을 변경할 때에는 Code, Data, Heap, Stack을 모두 옮겨야 하기 때문에 비용이 매우 비싸다.

반면, 스레드 단위의 컨텍스트 스위칭의 경우엔 Code, Data, Heap은 모두 공유하기 때문에 Stack 영역만 교체해주면 된다. 이로 인해, 상대적으로 컨텍스트 스위칭의 비용이 매우 저렴하다. (하지만 이는 상대적일 뿐, 스레드 간의 컨텍스트 스위칭도 오버헤드의 원인이기 때문에 최소화 하는 전략은 당연히 필요하다.)

동기화 문제

각 프로세스는 서로 간의 메모리 영역을 침범할 수 없기 때문에, 서로가 서로에게 문제를 일으키는 경우는 흔하지 않다. 

반면, 스레드의 경우는 모든 스레드가 Code, Data, Heap영역을 공유한다는 이유로 문제가 발생할 여지가 참 많다.

특정 스레드에서 A라는 변수의 값을 2로 바꾼다면, 다른 모든 스레드에게도 그 변화가 영향을 미칠 것이다. 만약, 어떤 스레드가 프로세스를 종료시켜버린다면? 다른 스레드도 모두 종료되어 버릴 것이다.

특히나 스레드를 여러개 사용하는 경우엔 스레드가 병렬적으로 작업하는 경우가 많은데, 서로의 작업 상황을 고려하지 않고 작업했다간 의도치 않은 문제가 발생할 수도 있다. (1번 스레드에서 해제한 메모리를 2번 스레드에서 참조한다면?)

이처럼, 스레드는 서로가 서로와 밀접하게 연관되어 있기 때문에 스레드를 여러개 사용할 때엔 세심한 주의가 필요하다.