어느 게임 개발자의 기록

문제를 먼저 보자.

최대 일 수 N과 챕터의 수 M이 주어진다.

챕터의 정보는 {소요 일 수, 페이지 수} 쌍으로 주어지며, N일동안 최대 몇페이지를 읽을 수 있는가? 를 찾는 문제이다.

입력이 아래와 같이 주어진다면

7 7
3 10
5 20
1 10
1 20
2 15
4 40
2 200

4번째 챕터 (1, 20), 6번째 챕터 (4, 40), 7번째 챕터(2, 200)을 읽으면

7일간 260페이지를 읽을 수 있고, 이 것이 읽을 수 있는 최대 페이지 수 이다.

문제 풀이

이 문제는 전형적인 DP문제이다. DP문제 중에서도 가장 유명한 문제를 꼽으라면 피보나치 수열과 배낭 문제를 꼽을 수 있는데, 이 문제는 배낭 문제와 완전히 동일한 문제이다.

배낭 문제가 궁금하다면, 찾아보는 것도 좋을 것 같다. 하지만, 본 문제와 완전히 동일하기 때문에 이 문제를 이해한다면 배낭 문제도 이해할 수 있을 것이다.

7 7
3 10
5 20
1 10
1 20
2 15
8 60
2 200

위의 입력을 기준으로 설명하도록 하겠다.

먼저, 표를 하나 그려보자.

가로는 최대 일 수를 의미하며, 세로는 챕터의 인덱스를 의미한다.

무슨 말인지 이해가 잘 안될 것이다.

자세히 설명하자면, 가로 인덱스가 1이라면 최대 일 수가 1이라고 가정을 한 상태에서 최대 페이지 수를 구한다는 것이다.

세로 인덱스는 1이라면, 1번 챕터까지 검사한 결과이고, 7이라면 7번 챕터까지 모두 검사한 결과라는 뜻이다.

(가로, 세로)가 (3, 5) 이라면 1~5번까지 챕터을 검사해서 최대 일 수가 3이라고 가정했을 때, 최대 페이지수가 몇인가? 를 구하는 것이다.

(가로, 세로)가 (6, 2) 이라면 1~2번까지 챕터을 검사해서 최대 일 수가 6이라고 가정했을 때, 최대 페이지수가 몇인가? 를 구하겠다는 것이다.

그렇다면, 이 표를 모두 갱신했을 때, (7, 7)이 결국 출력하고자 하는 답일 것이다.

최대 일 수인 7일동안 7개의 챕터를 모두 검사해서 최대 몇 페이지까지 읽을 수 있는가? 이게 (7, 7)의 값이기 때문이다.

일단, 표를 채우기 전에 논리적인 점화식을 세우고 가자.

먼저, 몇 가지 경우를 따져보자.

1. 현재 챕터를 읽을 수 없는 경우

현재 챕터를 읽을 수 있는 가, 없는 가에 대한 기준이 있을까?

만약, 최대 일수가 7일인데 한 챕터를 읽는데 8일이 걸린다면 그 챕터는 읽을 수가 없을 것이다.

이런 경우엔, 이 챕터를 포함하기 전의 최대값으로 갱신해주면 된다.

위의 입력을 보자. 6번 챕터는 읽는데 8일이 소요된다. 이런 경우 6번 챕터는 읽을 수 없기 때문에 0페이지를 읽는 것이나 마찬가지이다. 즉, 6번 챕터까지 검사한 최대 페이지 수는 5번챕터까지 검사한 최대 페이지 수와 동일할 것이다. 

2. 현재 챕터를 읽을 수 있는 경우

현재 챕터의 소요 일 수가 최대 일 수보다 적어서 읽을 수 있다면, 이 경우에도 두가지 경우의 수로 나뉜다.

 2 - 1. 해당 챕터를 읽지 않는 경우

 2 - 2. 해당 챕터를 읽는 경우

만약, 해당 챕터를 읽지 않겠다면 챕터를 읽을 수 없는 경우와 마찬가지로 이전 챕터까지 읽었을 때의 최대 페이지 수를 그대로 가져오면 된다.

하지만, 만약 챕터를 읽겠다면?

(최대 일 수 - 소요 일 수)를 최대 일수로 가정한 상황에서 이전 챕터까지 검사한 최대 페이지 수 + 현재 챕터의 페이지 수가 될 것이다.

이게 무슨 말이냐!!

보자. 현재 7일을 최대 일 수로 가정하고 있다고 해보자. 

여기서, 현재 챕터를 읽는데 4일이 소요된다고 한다면, 이 챕터를 읽고 남는 일 수는 3일이 된다.

즉 (이전 챕터까지 검사했을 때 3일간 읽을 수 있는 최대 페이지 수 + 현재 챕터의 페이지 수)가 해당 챕터를 읽었을 때의 최대 페이지 수가 될 것이다.

현재 챕터를 읽을 수 있는 경우에 최대 페이지 수는

std::max( 해당 챕터를 읽지 않는 경우의 페이지 수, 해당 챕터를 읽는 경우의 페이지 수) 가 되는 것이다.

아마 이해가 잘 안될 것이다. 표를 보며 다시 한 번 되새겨보자.

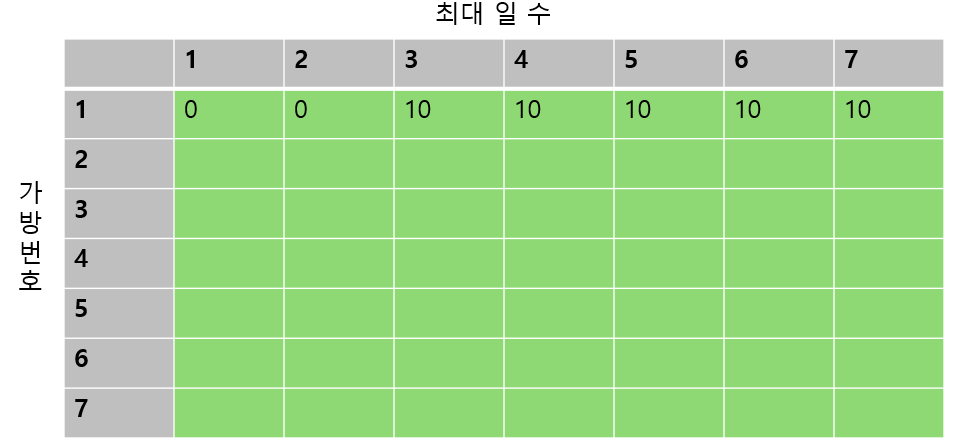
1번 가방까지에 대해서 표를 채워보면 이렇게 될 것이다.

최대 일수가 1일, 2일이라고 가정했을 땐, 1번 챕터를 읽을 수 없다.(소요 일수가 3일이기 때문에)

최대 일수가 3일 이상인 경우엔 1번 챕터 하나만 읽는 경우가 최대이기 때문에 10으로 모두 채워주면 된다.

이렇게 될 것이다.

먼저, 최대 일수가 1~4일 까진 2번 챕터를 읽을 수 없기 때문에 1번 챕터의 값을 그대로 가져오면 된다.

최대 일수가 5일이 될 때부턴 2번 챕터를 읽을 수 있다.

최대 일 수가 5일 일 때

-> std::max(2번 챕터를 안읽었을 때, 2번 챕터를 읽었을 때)가 표의 값에 들어갈 것이다.

2번 챕터를 안읽었을 때는 위칸의 값을 그대로 가져오면 되고,

2번 챕터를 읽었을 때는 1번 챕터까지 검사했을 때 0일동안 읽을 수 있는 최대 페이지 수 + 2번 챕터의 페이지 수이다.

위칸의 값은 10이고, 1번 챕터까지 검사했을 때 0일동안 읽을 수 있는 최대 페이지수 (0) + 2번 챕터의 페이지 수(20) 이므로 값은 20이 들어간다.

최대 일수가 6일 일 때

-> 2번 챕터를 안읽었을 때의 최대 페이지 수: 10

-> 2번 챕터를 읽었을 때의 최대 페이지 수 =

1번 챕터까지 검사했을 때 1일동안 읽을 수 있는 최대 페이지 수 + 2번 챕터의 페이지 수(20) : 20

최대 일수가 7일 일 때

-> 2번 챕터를 안읽었을 때의 최대 페이지 수: 10

-> 2번 챕터를 읽었을 때의 최대 페이지 수 =

1번 챕터까지 검사했을 때  2일동안 읽을 수 있는 최대 페이지 수 + 2번 챕터의 페이지 수(20) : 20

쭉쭉 채워보면, 

이렇게 될 것이고, 답은 우측 하단의 245가 될 것이다.

풀이 코드

입력 및 초기화

int MaxDays = 0;
int NumOfChapter = 0;

std::cin >> MaxDays >> NumOfChapter;

std::vector<std::vector<int>> DP(NumOfChapter + 1, std::vector<int>(MaxDays + 1, 0));
std::vector<std::pair<int, int>>Chapters(NumOfChapter + 1);

for (int i = 1; i <= NumOfChapter; i++)
{
    int Days = 0;
    int Pages = 0;
    std::cin >> Days >> Pages;

    Chapters[i] = { Days, Pages };
}

먼저, 최대 일 수와 챕터의 수를 입력받은 후 배열을 선언하였다.

배열은 직관적으로 사용하기 위해 +1만큼의 크기로 resize하였다.

(+1을 하지 않으면, 1이 0번 인덱스이고 2가 1번인덱스이기 때문에..)

이후, 챕터 정보를 입력받아 배열에 저장하였다.

for (int i = 1; i <= NumOfChapter; i++)
{
    for (int j = 1; j <= MaxDays; j++)
    {
        int CurDays = Chapters[i].first;
        int CurPages = Chapters[i].second;

        if (CurDays <= j)
        {
            DP[i][j] = std::max(DP[i - 1][j], DP[i - 1][j - CurDays] + CurPages);
        }
        else
        {
            DP[i][j] = DP[i - 1][j];
        }
    }
}

이후, 반복문을 돌며 검사하면 된다.

최대 일 수(j)를 기준으로 현재 챕터를 읽을 수 있다면, 읽지 않는 것과 읽는 것중 최대값으로 갱신하고

최대 일 수(j)를 기준으로 현재 챕터를 읽을 수 없다면, 이전 챕터까지 읽었을 때 최대 페이지 수를 그대로 가져오면 된다.

std::cout << DP[NumOfChapter][MaxDays];

이후, 가장 마지막 원소를 출력해주면 된다.

게임 내에서 여러 상호작용을 보면 물체간의 위치관계가 중요한 상황이 참 많다.

예를 들면, 몬스터의 시야 범위에 현재 들어와 있는가? (잠입 액션, 정찰 등)

내가 몹의 뒤에 서있는가? (백어택, 암살 등)

그렇다면 이런 위치관계를 어떻게 구해야 할까?

게임 프로그래밍에선 일반적으로 벡터의 내적과 외적을 이용하여 구한다.

이 내용을 이해하려면 벡터에 대한 기본적인 개념이 있어야 한다.

벡터에 대한 지식이 없다면 찾아보고 나서 읽는 것을 추천한다.

먼저 이런 위치 관계예 놓여있다고 하자.

좌표상으로만 보면, 몹은 나의 위에있고 오른쪽에 있는 것이다.

하지만, 이건 절대적인 좌표의 기준일 뿐이고 만약 내가 왼쪽을 보고있다면?

아래 사진처럼 왼쪽을 바라보며 서있다면, 몹은 나의 뒤에 존재하게 되고, 나의 오른쪽에 존재하게 된다.

즉, 몹과 나의 방향 관계를  정확히 파악하려면 먼저 바라보고 있는 방향에 대한 벡터가 필요하다.

방향 벡터를 구하는 것은 어렵지 않다.

먼저, 플레이어의 위치, 회전관계를 전혀 건드리지 않았을 때 최초에 바라보는 방향이 필요하다.

아마 일반적인 상태에선 최초에 바라보는 방향에 대한 벡터는 (0, 0, 1)일 것이다.

(매쉬에 따라 다를 수 있고, 엔진 환경에 따라 다를 수 있다. 다만, 최초에 바라보고 있는 방향 벡터라는 것만 알면 된다.)

이런 상황에서 플레이어가 x축으로 60도만큼 회전했다면?

바라보는 방향에 대한 벡터 또한 x축으로 60도만큼 같이 회전할 것이다.

즉, 플레이어의 현재 회전값만큼 항상 함께 회전하기 때문에 (0,0,1)벡터를 플레이어의 회전 값만큼 회전시키면

그게 현재 플레이어의 정면 벡터인 것이다.

정면에 대한 벡터는 이렇게 구해보았다. 그렇다면 다음은 무엇을 해야 할 까.

아래 사진을 보자. 보라색 벡터는 플레이어로부터 몹을 향하는 벡터이다.

정면을 향하는 벡터와 몹을 향하는 벡터 사이의 각 (Theta)가 90도보다 크다면, 몹은 뒤에 있다고 할 수 있지 않을까?

반대로, Theta가 90도 보다 작다면, 몹이 내 앞에 있다고 할 수 있지 않을까?

그렇다. 노란색 벡터(정면에 대한 벡터)와 보라색 벡터(몹을 향한 벡터) 사이의 각도를 구하면 몹이 앞에 있는지 뒤에 있는 지를 판별할 수 있다.

일단, 각도를 구하기 전에 보라색 벡터(몹을 향한 벡터)를 구해보자.

이건 간단하게 구할 수 있다.

(몹의 위치 좌표 - 나의 위치 좌표)가 보라색 벡터이다.

벡터의 뺄셈 연산을 알고있다면 이해하는 것에 무리는 없을 것이다.

이렇게, 정면 벡터와 몹을 향한 벡터를 구했다면 두 벡터 사이의 각을 구하면 된다.

그런데, 그 전에 한가지 알고 넘어가야 하는 사실이 있다.

바로 몹과 나의 y축 좌표(위, 아래)를 고려해야 하는가? 에 대한 문제이다.

나의 정면 벡터는 정상적으로 서있다면, 항상 지면에 수평이다.

하지만, 나와 몹의 높이 차이가 존재한다면 몹을 향한 벡터는 지면에 수평이지 않을 수 있다.

즉 두 벡터 사이의 각도가 우리가 의도하는 것과는 다르게 나올 수 있다는 것이다.

단순히 몹이 내 앞에 있는가? 뒤에 있는가? 만을 고려한다면 y값의 차이는 계산에 영향을 미쳐선 안된다.

그렇기 때문에, 정면 벡터의 y값을 0으로, 몹을 향한 벡터의 y값을 0으로 하여 x와 z만을 가지고 계산하는 것이 일반적으로 옳다.

그렇게 y값을 제거한 뒤, 두 벡터를 구했다면 이제 각도만 구하면 된다.

각도는 벡터의 내적을 이용하여 구하면 된다.

A · B =  벡터A의 길이 * 벡터B의 길이 * Cos(Theta)이다.

여기서 길이의 곱만 제거한다면 Cos(Theta)만 남을 것이다.

그렇기 때문에, 두 벡터를 내적하기 이전에 먼저 정규화(노말라이즈)를 해주어야 한다.

정규화란 벡터의 길이를 1으로 맞추는 작업이며 벡터의 크기의 영향을 제거하고 방향만을 가지고 계산을 하기 위한 연산이다.

정규화는 어렵지 않다.

벡터의 x,y,z 성분을 벡터의 크기로 나누어 주면 끝이다.

벡터의 크기가 L이라면, (x/L, y/L, z/L)이 정규화된 벡터이다.

이렇게, 정면 벡터와 몹을 바라보는 두 벡터를 정규화 하였다면, 두 벡터를 내적해주자.

내적은 각 성분을 모두 곱해주면 된다.

(X1, Y1, Z1), (X2, Y2, Z2) 두 벡터가 있다면, (X1 * X2 + Y1 * Y2 + Z1 * Z2)가 두 벡터의 내적 값이다.

이렇게, 정면 벡터와 몹을 바라보는 두 벡터를 내적하였다면, 그 값은 Cos(Theta)일 것이다.

A · B =   (X1 * X2 + Y1 * Y2 + Z1 * Z2)  = 벡터A의 길이 * 벡터B의 길이 * Cos(Theta) 이고, 두 벡터의 길이는 1이므로

A · B =   (X1 * X2 + Y1 * Y2 + Z1 * Z2)  = Cos(Theta)

여기서, acos함수를 이용하여 Theta를 정확히 구할 수도 있지만 사실 불필요한 연산이다.

Cos함수의 경우 각도에 따른 값의 범위가 명확히 정해져 있다.

0 <= Theta < 90 이라면, 0 < Cos(Theta) <= 1 이고

90 <= Theta < 180 이라면, -1 < Cos(Theta) <= 0 이 될 것이다.

즉, 두 벡터를 내적한 값이 0과 1 사이라면, 몹은 내 앞에 있는 것이며

-1과 0 사이라면 나의 뒤에 있는 것이라고 판별할 수 있다.

하지만, 이렇게 내적으로 몹과 나의 위치관계를 구하게 되면 한 가지 문제가 있다.

내적은 0~180도 범위에서만 작동한다.

저렇게 몹이 반대편에 위치한다고 하더라도 값은 똑같이 나온다.

즉, 앞 뒤는 구별할 수 있어도 왼쪽 오른쪽은 구별할 수 없다는 뜻이다.

그렇다면 왼쪽 오른쪽은 어떻게 구할까?

간단하다. 정면벡터와 몹을 향하는 방향 두 벡터를 외적해보면 된다.

두 벡터의 y값을 제거하고 지면에 수평인 벡터로 만들어 준다.

그리고 두 벡터를 외적하면 지면에 수직힌 벡터가 나올 것이다.

두 벡터의 위치 관계에 따라, 지면 위로 솟아나는 방향일 수도 있도, 지면 안쪽으로 들어가는 방향일 수도 있다.

무조건, 정면 벡터를 앞에 두고 ( 정면 벡터 x 몹을 향한 벡터 ) 이렇게 외적을 해보자.

오른손 법칙에 의해, 몹을 향한 벡터가 정면 벡터보다 왼쪽을 향하고 있다면 위로 솟아나는 벡터가 나올 것이고

몹을 향한 벡터가 정면 벡터보다 오른쪽을 향하고 있다면 아래로 들어가는 벡터가 나올 것이다.

즉, 두 벡터를 외적한 벡터의 y값이 양수이면 왼쪽, 음수이면 오른쪽 이라고 판별할 수 있다.

그림에도 나와 있듯이, 정면 벡터(u) 를 기준으로 했을 때, 몹을 향한 벡터(v)가 왼쪽에 위치한다면 외적한 벡터는 위를 향할 것이다.

당연히, 오른쪽에 있다면 외적한 벡터는 아래를 향할 것이다.

다만 아주 중요한 점이 있다

위에선 오른손을 기준으로 외적의 뱡향을 설명했지만, 항상 이 기준이 오른손이 되는 것이 아니다. 좌표계를 어떻게 정의하느냐에 따라 달라질 수 있다. DirectX, Unreal Enigne, Unity에선 왼손을 기준으로 계산 해야한다!반면, OpenGL, Vulkan 등에선 오른손을 기준으로 계산 해야한다!

이렇게, 내적과 외적을 활용해서 다른 오브젝트와 나의 위치 관계를 구해보았다.

게임을 프로그래밍하다 보면, 내적과 외적은 정말 활용할 곳이 너무너무 많다.

반드시 알아야만 한다!

객체지향 디자인 패턴에는 팩토리 메서드 패턴과 추상 팩토리 패턴이 있다.
두 패턴에 대해 알아보기 전에 먼저 심플 팩토리에 대해 알아보자.

심플 팩토리는 두 디자인 패턴의 기본이 되는 방식이다.

객체지향 원칙을 다소 위배하는 부분이 있어, 디자인 패턴으로 분류되지는 않고 일종의 관용구라고 생각하면 좋다.

그리고, 이 패턴의 단점을 해결한 패턴이 팩토리 메서드 패턴과 추상 팩토리 패턴인 것이다.

심플 팩토리란?

먼저, 이 패턴이 왜 나왔는지에 대해 이해해보자.

음료수를 마시고 싶은 손님과 이를 판매하는 상황을 예로 들어보겠다.

소비자는 Client클래스이며, 음료수는 GrapeBeverage, AppleBeverage 두 객체가 있다고 해보자.

일반적으로는 이렇게 음료수 객체를 생성할 것이다.

class Client
{
    void BuyBeverage()
    {
    	GrapeBeverage* GrapeBG = new GrapeBeverage();
    	AppleBeverage* AppleBG = new AppleBeverage();
    }
};

이렇게, new를 통해 객체를 직접적으로 생성하게 되면 객체지향적인 부분에서 문제가 생긴다.

Client 객체와 음료수 객체 간의 결합도가 높아진다는 것이다.

지금이야 코드가 간단하니 괜찮아 보여도 코드 길이가 길어진다고 가정해보면, GrapeBeverage, AppleBeverage 객체를 수정하게 될 때 그에 따라서 Client의 코드를 수정해야 하는 상황도 심심찮게 발생할 것이다.

이러한 결합도, 의존성을 제거하기 위해 만들어진 것이 심플 팩토리 패턴이다.

그렇다면 심플 팩토리 패턴은 어떤 방식으로 설계해야 할까?

class Beverage
{
public:
    virtual void Drink() = 0;
};

class GrapeBeverage : public Beverage
{
public:
    void Drink()
    {
        std::cout << "포도 주스를 마셨다." << std::endl;
    }
};

class AppleBeverage : public Beverage
{
public:
    void Drink()
    {
        std::cout << "사과 주스를 마셨다." << std::endl;
    }
};

먼저 이렇게 음료수를 상속 구조로 바꿔보자.

GrapeBeverage와 AppleBeverage는 모두 Beverage 클래스를 상속받고 있다.

이번엔, 이 음료수를 생성해주는 클래스를 만들어 볼 것이다.

class BeverageFactory
{
public:
    enum class BeverageType
    {
        Grape,
        Apple,
    };

    Beverage* CreateBeverage(BeverageType _InputType)
    {
        Beverage* ReturnBeverage = nullptr;

        switch (_InputType)
        {
        case BeverageType::Grape:
            ReturnBeverage = new GrapeBeverage();
            break;
        case BeverageType::Apple:
            ReturnBeverage = new AppleBeverage();
            break;
        }

        return ReturnBeverage;
    }
};

이렇게 enum타임만 입력받으면 내부에서 음료수는 만들어서 부모 클래스 타입으로 반환해주는 클래스를 만들게 된다면

Client클래스에선 BeverageFactory 클래스 하나만 알아도 모든 종류의 음료수를 다 만들 수 있는 것이다.

이제 위의 클라이언트 코드를 수정해보면

class Client
{
public:
    void BuyBeverage()
    {
        BeverageFactory* BGFactory = new BeverageFactory();

        Beverage* GrapeBG = BGFactory->CreateBeverage(BeverageFactory::BeverageType::Grape);
        Beverage* AppleBG = BGFactory->CreateBeverage(BeverageFactory::BeverageType::Apple);

        GrapeBG->Drink();
        AppleBG->Drink();
    }
};

Beverage와 BeverageFactory클래스만 알고 있다면,

음료수의 종류가 100개가 되든 200개가 되든 직접적인 결합 없이 생성할 수 있게 되는 것이다.

이 것이 심플 팩토리 패턴이다.

객체를 직접 알지 않아도 생성할 수 있도록 하는 것이다.

다만, 이 심플 팩토리 패턴의 경우엔 위에서 말했듯이 객체지향의 원칙을 위반하는 것이 있다.

개방-폐쇠 원칙에 위배된다.

왜냐면, 음료수를 추가할 때마다 CreateBeverage 내부의 함수를 고쳐야 한다.

물론 switch 분기 하나 추가하는 정도긴 하지만, 객체지향 원칙을 제대로 지키려면 개방에는 열려있어야 하지만 수정에는 닫혀있어야 한다.

이 문제를 커버하기 위해 나온 패턴이 팩토리 메서드 패턴과 추상 팩토리 패턴이다.

팩토리 메서드 패턴

팩토리 메서드 패턴은 심플 팩토리 패턴을 기반으로 설계된다.

먼저 어떻게 설계되는지 보자.

class BeverageFactory
{
public:
    virtual Beverage* CreateBeverage() = 0;
};

BeverageFactory를 위와 같이 추상 클래스로 선언해준다.

class GrapeBeverageFactory : public BeverageFactory
{
public:
    virtual Beverage* CreateBeverage() override
    {
        Beverage* ReturnBeverage = new GrapeBeverage();
        return ReturnBeverage;
    }
};

class AppleBeverageFactory : public BeverageFactory
{
public:
    virtual Beverage* CreateBeverage() override
    {
        Beverage* ReturnBeverage = new AppleBeverage();
        return ReturnBeverage;
    }
};

이후, 이렇게 BeverageFactory를 상속받은 클래스를 각각 만들고, 각 클래스가 하나의 음료만 담당하도록 하자.

Client에선 아래와 같이 사용한다.

class Client
{
public:
    void BuyBeverage()
    {
        BeverageFactory* GrapeBGFactory = new GrapeBeverageFactory();
        BeverageFactory* AppleBGFactory = new AppleBeverageFactory();

        Beverage* GrapeBG = GrapeBGFactory->CreateBeverage();
        Beverage* AppleBG = AppleBGFactory->CreateBeverage();

        GrapeBG->Drink();
        AppleBG->Drink();
    }
};

이런 식으로 각 음료당 하나의 클래스를 담당하여 Factory클래스를 구성하게 되면, 음료룰 추가할 때 객체의 코드를 구성할 필요가 없고 새로운 클래스를 하나 더 추가하면 된다.

즉 개방-폐쇄 원칙을 위반하지 않는 셈이 된다.

다만, 이 패턴의 단점은 음료의 수가 많아질수록 관리해야 하는 클래스가 점점 많아진다는 것이다.

그런 단점에도 불구하고 의존성 분리에 있어 효과적인 디자인 패턴이기 때문에 의외로 많은 곳에서 접할 수 있는 패턴이다.

추상 팩토리 패턴

추상 팩토리 패턴은 팩토리 메서드 패턴과 거의 유사한 패턴이다.

이번엔 음료수를 하나 사면 경품도 추가로 준다고 가정해보자.

포도 주스를 구매하면 포도 빵을 주고 사과 주스를 사면 사과 빵 준다고 가정해보겠다.

class Bread
{
    virtual void Eat() = 0;
};

class GrapeBread : public Bread
{
    virtual void Eat() override
    {
        std::cout << "포도 빵을 먹었다" << std::endl;
    }
};

class AppleBread : public Bread
{
    virtual void Eat() override
    {
        std::cout << "사과 빵을 먹었다" << std::endl;
    }
};

먼저 이렇게 빵을 선언해주자.

이후, BeverageFactory 클래스에 순수가상함수를 하나 추가해주겠다.

class BeverageFactory
{
public:
    virtual Beverage* CreateBeverage() = 0;
    virtual Bread* CreatePrize() = 0;
};

이후 이 클래스를 상속받은 하위 클래스들이 구현해주면 끝이다.

class GrapeBeverageFactory : public BeverageFactory
{
public:
    virtual Beverage* CreateBeverage() override
    {
        Beverage* ReturnBeverage = new GrapeBeverage();
        return ReturnBeverage;
    }

    virtual Bread* CreatePrize()
    {
        Bread* ReturnBread = new GrapeBread();
        return ReturnBread;
    }
};

class AppleBeverageFactory : public BeverageFactory
{
public:
    virtual Beverage* CreateBeverage() override
    {
        Beverage* ReturnBeverage = new AppleBeverage();
        return ReturnBeverage;
    }

    virtual Bread* CreatePrize()
    {
        Bread* ReturnBread = new AppleBread();
        return ReturnBread;
    }
};

언뜻 보기엔 팩토리 메서드 패턴과 대체 뭐가 다르지? 싶다.

다른 점은 하나이다. 연관된 객체들을 함께 관리할 수 있다는 것이다.

class Client
{
public:
    void BuyBeverage()
    {
        BeverageFactory* GrapeBGFactory = new GrapeBeverageFactory();
        Beverage* GrapeBG = GrapeBGFactory->CreateBeverage();
        Bread* GrapeBread = GrapeBGFactory->CreatePrize();
        
        GrapeBG->Drink();
        GrapeBread->Eat();

        BeverageFactory* AppleBGFactory = new AppleBeverageFactory();
        Beverage* AppleBG = AppleBGFactory->CreateBeverage();
        Bread* AppleBread = AppleBGFactory->CreatePrize();

        AppleBG->Drink();
        AppleBread->Eat();
    }
};

위와 같이, 하나의 팩토리가 가진 멤버함수를 사용하여 연관된 객체를 고민없이 생성할 수 있다.

예를 들어 캐릭터가 여러 종류 있고, 캐릭터 별로 따라다니는 펫의 종류가 다르다고 한다면

현재 캐릭터와 매칭되는 펫이 무엇인지 고민할 필요 없이 팩토리에서 펫을 만들어주는 함수만 호출하면 되는 것이다.

팩토리 메서드 패턴에서 더 캡슐화된 형식이라고 보면 될 것 같다.

여기까지 팩토리 메서드 패턴과 추상 팩토리 패턴에 대해 알아보았다.

다음 게시물에선 컴포넌트 패턴을 올려볼까 한다.

문제는 이러하다.

각 칸에는 가중치가 입력되어 있으며, 해당 발판에서는 가중치만큼 오른쪽 혹은 아래로 이동할 수 있다.

규칙대로 이동하여 도착지점(우측 하단)에 도착할 수 있는 경우의 수를 구하면 된다.

문제 풀이

본인은 DFS와 DP를 사용하여 풀었다.

DFS, DP에 대해 모른다면, 찾아보고 오는 것을 추천한다.

먼저 예제 입력을 보자.

입력에 대한 맵과 동일한 크기의 DP배열을 만들어 놓았다.

좌측이 입력받은 배열이며, 우측이 DP배열이다.

먼저 한 가지 방향으로 먼저 쭉 진행해보자.

이런 방향으로 이동할 수 있을 것이다.

도착 했으니, DP배열의 도착지점의 값을 1로 바꿔주겠다.

도착했으니, 뒤로 돌아오며 다음 길을 탐색해야 한다.

돌아오면서, 다음 위치의 DP배열 값을 이전 위치에 더해줄 것이다.

예를 들어, (1,1)에서 (0,0)으로 돌아갈 때, DP배열의 (1,1) 값이 2였다면, DP배열의 (0,0) 값에 2를 더해줄 것이다.

DP배열의 값은 해당 좌표로부터 도착 지점(우측 하단)까지 탐색된 경로의 수를 의미한다.

이렇게 말이다.

그럼, 다음 길을 다시 찾아보자.

이런 경로도 있을 것이다.

근데, 마지막 빨간색 화살표는 보면 도착 지점의 DP배열의 값이 0이 아니다.

즉 이미 그 이후의 길을 탐색한 적이 있다는 것이며, 다시 탐색할 이유는 없다는 것이다.

그대로 다시 뒤로 돌아가며 다음 길을 탐색하자.

물론 돌아가면서 DP의 값도 갱신해줄 것이다.

여기까지 갱신하며 돌아왔다면, 다음 길을 찾을 수 있다.

이렇게 다음 길을 진행할 수 있다.

빨간색 화살표를 보면, 위에서 말했듯이 굳이 탐색할 필요가 없다.

그대로 돌아오며 DP를 갱신해주자.

돌아오며, 값을 더해주며 돌아오면? 오른쪽처럼 (0,0)의 값이 3이 되어있다.

답은 3이다. 그대로, Dp배열의 (0,0) 값을 출력해주면 된다.

풀이 코드

int Width = 0;
std::vector<std::vector<int>> Board;
std::vector<std::vector<long long>> DP;

먼저, 입력을 저장할 Width, Board를 선언하고

DP배열까지 선언해주자.

std::cin >> Width;

Board.resize(Width, std::vector<int>(Width, 0));
DP.resize(Width, std::vector<long long>(Width, 0));

for (int i = 0; i < Width; i++)
{
    for (int j = 0; j < Width; j++)
    {
        std::cin >> Board[i][j];
    }
}

이후, resize 해준 뒤에 입력을 저장해주면 된다.

DFS(0, 0);

std::cout << DP[0][0];

return 0;

그 이후엔, 이렇게 간단하게 DFS함수 하나만 호출해주고 (0, 0)의 값을 출력해주면 된다.

아래는 DFS함수의 코드 전문이다.

long long DFS(int _X, int _Y)
{
    if (_X == Width - 1 && _Y == Width - 1)
    {
        return 1;
    }
    
    if (Board[_Y][_X] == 0)
    {
        return 0;
    }
    
    if (DP[_Y][_X] != 0)
    {
        return DP[_Y][_X];
    }
    
    int CurWeight = Board[_Y][_X];
    
    {
        int NextRightX = _X + CurWeight;
        int NextRightY = _Y;
    
        if (NextRightX < Width && NextRightY < Width)
        {
            DP[_Y][_X] += DFS(NextRightX, NextRightY);
        }
    }
    
    {
        int NextDownX = _X;
        int NextDownY = _Y + CurWeight;
    
        if (NextDownX < Width && NextDownY < Width)
        {
            DP[_Y][_X] += DFS(NextDownX, NextDownY);
        }
    }
    
    return DP[_Y][_X];
}

우측과 좌측을 탐색하며, 재귀적으로 함수를 호출한다.

먼저, 가장 위의 조건문을 보면 도착지점에 도착했다면 DP배열의 값을 1로 바꾼 뒤, 함수를 return한다.

두 번째 조건이 중요하다. 본인은 저 조건문을 추가하지 않아서 메모리 초과가 뜬 경우가 있었다.

가중치가 0이라면, 오른쪽이든 아래쪽이든 이동하지 못하고 무한 루프를 돌기 때문에, 반드시 예외처리를 해주어야 한다.

세번째 조건문은 현재 위치로부터 도착지점까지 이미 탐색한 경로가 있다면, 굳이 한 번 더 탐색하지 않기 위한 조건문이다. 위에서 설명했듯이 DP배열의 값은 해당 위치로부터 도착ㄹ지점까지 이어진 경로의 수를 의미하며, 이미 탐색한 적이 있다면 굳이 한 번 더 탐색할 이유는 없다.

이 3가지 조건문을 뚫고 아래까지 도달했다면, 이제 우측과 아래쪽에 대해 탐색을 진행하면 된다.

이 문제에서 주의해야 할 점은 두가지이다.

1. 가중치가 0일 때 예외처리를 해주어야 한다.

2. DP 배열의 값은 int가 아니라 long long으로 저장해야 한다.

DFS를 알고 있다면, 크게 어려운 문제는 아니지만 처음 접하면 다소 헷갈릴 수 있는 문제이다.

이런 문제는 필자처럼 직접 경우의 수를 그려보며 생각하면 이해가 쉽게 될 것이다.

객체지향 디자인 패턴에는 싱글톤이라는 패턴이 있다.

싱글톤이란?

어떠한 클래스의 인스턴스가 프로세스 내에 단 1개만 생성되도록 제한하는 디자인 패턴.

예를 들면, 게임 내에서 플레이어가 있고 이 플레이어가 지니고 있는 스텟이 있다고 했을 때, 플레이어의 스텟 정보는 다음 레벨로 넘어가더라도 유지되어야 한다.

하지만, 플레이어 객체 내부에 스텟 데이터를 저장해두었다면 레벨이 바뀌는 순간, 객체는 파괴되어버리고 스텟 데이터는 사라지게 된다. 다음 레벨에서 스폰되는 플레이어 객체는 기존과는 다른 스텟 데이터를 가지고 있게 되는 것이다.

이러한 이유로 게임 프로그래밍에선 데이터를 가능한 분리하는 것이 좋다. 

그렇다면, 스텟 정보를 다른 클래스로 분리를 시켰는데 이 클래스가 여러개가 있어야 할까?

플레이어의 Hp, 공격력 등의 정보를 담은 클래스의 인스턴스는 게임에 1개만 있으면 충분하다. 2개 3개가 되면 메모리만 낭비될 뿐이다.

이런 상황에 데이터 정보를 담은 클래스의 인스턴스를 단 1개로 제한하기 위해 사용할 수 있는 디자인 패턴이 싱글톤 패턴이다.

어떻게 사용하는가?

방식은 여러가지가 있다.

먼저 가장 간단한 방식이다.

1. 이른 초기화

class Singleton
{
    private:
        Singleton() {}
        ~Singleton() {}
        
        static Singleton instance;

    public:
        static Singleton &GetIstance()
        {
            return instance;
        }
};

Singleton Singleton::instance;

생성자와 소멸자를 private로 선언하여, 외부에서 생성 및 소멸을 할 수 없도록 한다.

이후, static으로 전역 변수를 선언하여 인스턴스를 생성해준다.

다른 클래스에서 싱글톤 객체를 참조하고 싶다면, Singleton::GetInstance() 함수를 호출하여 참조자를 반환받아 사용한다.

아주 간단하게 객체를 단 1개만 생성되도록 해보았다.

소멸자와 생성자가 private이기 때문에 객체의 생성은 내부에서만 가능하다.

내부에서는 static으로 단 1개만 생성하였기 때문에 프로세스 내에는 인스턴스가 1개만 존재하게 된다.

하지만, 이 경우 문제가 몇가지 있다.

1. 전역 변수의 생성, 초기화 시기는 정확히 정의되어 있지 않다.

C++에서 전역변수를 여러개 선언하게 된다면, 이 객체들의 생성 시기는 정확하게 정해져 있지 않다.

A, B, SingleTon 이렇게 3개의 전역 변수를 선언했다고 가정하면

A->B->SingleTon 순서로 생성될 수도 있지만, B->SingleTon->A 의 순서로 생성될 수도 있는 것이다.

만약, A의 생성자에서 SingleTon을 참조했다고 가정해보자.

SingleTon->A->B 의 순서로 전역 객체가 생성되었다면 별 다른 문제가 없지만

A->SingleTon->B의 순서로 생성된다면 문제가 발생한다. A에서 참조하고자 하는 대상이 아직 존재하지 않기 때문이다.

이런 경우는 흔하지 않은 경우지만, 이른 초기화 방식이 안전하지 않음을 명확히 알고 있어야 한다.

2. 프로세스가 시작되는 순간부터 끝나는 순간까지 메모리를 계속 점유한다.

싱글톤 객체가 자주 사용되고 계속 참조된다면 상관이 없지만, 자주 사용되지 않는다고 한다면 이는 비효율적일 수 있다.

처음부터 전역변수로 생성되고 프로세스가 끝날 때 까지 계속 메모리 상에 존재하기 때문에 메모리 낭비가 발생할 수 있는 것이다.

이러한 문제점을 해결하기 위해 나온 두 가지 방식이 있다.

2. 늦은 초기화 - 다이나믹 싱글톤

class Singleton
{
    private:
        Singleton() {}     
        ~Singleton() 
        {
            delete Instance;
            Instance = nullptr;
        }
        
        static Singleton* Instance;

    public:
        static Singleton* GetIstance()
        {
            if(Instance == nullptr)
            {
                Instance =  new Singleton();
            }
            
            return Instance;
        }
};

Singleton* Singleton::Instance = nullptr;

먼저, 늦은 초기화의 한 종류인 다이나믹 싱글톤이다.

이 방식은 GetInstance가 호출되는 시기에,  Instance이 nullptr인지 아닌지를 검사하게 된다.

Instance가 nullptr이라면 그 시기에 객체를 생성하여 참조할 수 있게 해준다.

즉, 이른 초기화 방식에서 발생할 수 있었던 생성 시기의 문제가 해결되는 것이다.

또한, GetInstance()를 호출하기 전까지 객체가 생성되지 않기 때문에 메모리를 효율적으로 사용할 수 있다.

다만, 이 방식도 두 가지 문제가 있다.

1. Thread-Safe 하지 않다는 것

멀티스레딩 환경에서 서로 다른 스레드가 동시에 GetInstance()함수를 호출한다고 가정해보자.

A스레드가 GetInstance()를 호출하고 Instance가 nullptr임을 확인하고 동적할당을 실행하였다.

동적할당이 완료되기 전 B스레드가 GetInstance()를 호출한다면 여전히 Instance는 nullptr이기 때문에

B스레드 또한 동적 할당을 실행할 것이다.

즉, 객체를 한개만 만들기 위한 디자인 패턴임에도 불구하고 멀티스레딩 환경에선 객체가 2개 이상 생성될 수 있다는 것이다. 물론, lock_guard, mutex등을 사용하여 방지할 수는 있지만 이러한 경우 성능 저하를 유발할 수 있기 떄문에 좋은 방법은 아니다.

2. 소멸자 호출 시기가 불 분명하다는 것

위에서 말했듯이 전역변수는 생성 시기가 명확하지 않다. 당연히, 소멸 시기또한 명확하지가 않다.

소멸자에서 메모리 해제를 해주고 있는데, 이는 소멸 시기에 따라 메모리 누수로 기록될 수 있다.

그렇기 때문에 프로세스가 끝나기 전에 명시적으로 메모리 해제 함수를 호출하여 직접 delete를 해주어야 하고, 여기서 번거로움이 발생할 수 있다.

이를 해결하기 위한 또 하나의 늦은 초기화 방식이 있다.

2. 늦은 초기화 - 마이어스 싱글톤

class Singleton
{
    private:
        Singleton() {}     
        ~Singleton() {}

    public:
        static Singleton& GetIstance()
        {
            static Singleton Instance;
            return Instance;
        }
};

이렇게 지역 스태틱 변수를 활용하는 것이다.

이는 동적할당을 하지 않기 때문에, 메모리 누수로 기록될 여지도 없으며, static 변수는 두 개 이상 생성 될 수 없기 때문에 thread-safe하다.

또한, GetInstance()가 호출되기 전까지 객체가 생성되지도 않으므로 메모리 낭비 또한 걱정할 필요 없는 방식이다.

하지만, 여전히 한 가지 문제는 남아있다.

소멸자 호출 시기가 불 분명하다는 것

위에서 여러 번 언급했듯이, 전역 객체는 소멸과 생성의 시기가 정확하지가 않다. 이렇게 GetInstance() 호출 시 생성되는 방식으로 생성 시기의 불분명함으로 발생하는 문제는 해결할 수 있지만, 소멸 시기의 불분명함으로 발생하는 문제는 해결할 수 없다. 

다른 전역 객체의 소멸자에서 GetInstance()를 호출하는 시기에 SingleTon 객체가 소멸했다면 여기서 문제가 발생한다.

(물론 이런 상황은 정말 흔하지는 않겠지만...)

이러한 소멸자의 문제를 해결하기 위해, 피닉스 싱글톤이라는 좀 더 어려운 방식이 존재한다.

3. 피닉스 싱글톤

class PhoenixSingleton
{
private:    
    static bool bDestroyed;   
    static PhoenixSingleton* pIns;     
    PhoenixSingleton() {};    
    PhoenixSingleton(const PhoenixSingleton& other);    
    ~PhoenixSingleton()   
    {        
        bDestroyed = true;    
    }
    
    static void Create()   
    {        
        static PhoenixSingleton ins;        
        pIns = &ins;    
    }
    
    static void KillPheonix()   
    {        
        pIns->~PhoenixSingleton();    
    }
    
public: 
    static PhoenixSingleton& GetInstance()   
    {        
        if (bDestroyed)        
        {            
            new(pIns) PhoenixSingleton;            
            atexit(KillPheonix);           
            bDestroyed = false;       
        }       
        else if (pIns == NULL)      
        {           
            Create();       
        } 
        
        return *pIns;  
    }
}; 

bool PhoenixSingleton::bDestroyed = false;
PhoenixSingleton* PhoenixSingleton::pIns = NULL;

싱글톤 객체가 소멸된 상태에서 호출되면 다시 객체를 되살리는 방식이다.

전역 변수인 bDestroyed를 이용하여 객체가 살아있나 죽어있나를 판단한 뒤, 객체가 죽어있는 상태라면

placement new를 사용하여 객체를 다시 되살린다. (전역 변수는 소멸 시기에 메모리를 초기화하지 않는다고 한다.)

이후 atexit함수를 이용하여, 프로그램 종료 시기에 소멸자가 호출될 수 있도록 한다.

placement new로 할당한 메모리는 delete로 해제하는 것이 아니라 소멸자를 직접 호출해야 한다.

이 방식도 완전히 문제가 없는 것은 아니라는데, 사실 그 정도까지 들어갈 필요가 있나 싶다.

피닉스 싱글톤을 사용하고 나서도 문제가 발생한다면, 싱글톤 구조를 고민하기보단 코드 설계를 제대로 했는가를 먼저 고민해보도록 하자...

이렇게 여러가지 싱글톤을 알아보았는데, 싱글톤은 사용하기에 따라 편리하고 유용한 디자인 패턴이기도 하지만

몇 가지 단점들로 인해 안티 패턴이라고 여겨지기도 한다.

1. 객체의 결합도가 높아진다. (의존성이 높아진다.)

싱글톤 같은 경우, 전역 함수를 통해 인스턴스를 받아온 뒤, 정적 메소드를 직접 호출하게 된다.

ex) InfoManager::GetInstance()->GetLevel();

이런 방식의 경우, 객체 간의 결합도가 높아지게 되고 싱글톤 객체의 코드를 수정하게 되면 이를 참조하는 수많은 객체의 코드를 모두 수정해야 할 수도 있다. 객체지향적인 측면에서 싱글톤 패턴은 그리 좋은 설계는 아니라는 것이다.

2. 멀티 스레딩 환경에서 안정적이지 못하다.

싱글톤 방식같은 경우, 하나의 객체를 여기저기서 참조하게 된다. 읽기만 하는 것이 아니라 경우에 따라 쓰기를 할 때도 있다. 멀티 스레딩 환경에선 하나의 메모리 영역을 여기저기서 공유하게 되니, 동기화에 대한 중요성이 커지게 된다. 이를 해결하기 위해, 여기저기에 동기화 처리를 해주게 되면 성능이 많이 저하될 수 있다. 

싱글톤 패턴은 이러한 문제점들 때문에 효율적으로 설계하기 참 까다로운 패턴이다.

구현이 간단하다고 해서 아무렇게나 사용하지 말고, 사용에 있어 고민을 많이 해보아야 할 듯 하다.

가로 길이가 n으로 주어질 때, 가능한 경우의 수는 몇개인가? 를 구하는 문제이다.

예를 들어 n이 3이라고 가정해보자.

이런 3개의 경우의 수가 가능할 것이다.

 n개일 때는 경우의 수가 몇개인지를 구하려면 어떻게 해야할까?

문제 풀이

이 문제는 기본적인 DP문제이다. 사실 DP문제는 어떠한 알고리즘이 있다기보단, 창의력이나 사고력을 요하는 경우가 더 많은 것 같다. 하지만, 자주 나오는 유형들을 보면 대부분 점화식을 이용하여 다음 항을 유추하는 케이스와 완전탐색과 함께 사용하는 케이스가 가장 많은 것 같다. 자주 풀어보면 감이 올 것이다.

이 문제는 먼저 점화식을 세워야 한다.

먼저, n개의 타일을 배치하는 여러 개의 경우의 수가 있다고 했을 때 모든 경우의 수를 고려하는 것이 아니라 딱 2개의 경우로만 나눠보자.

크게 두 개의 경우로 나누어 보자.

1. 맨 앞의 블럭이 서있는 경우

2. 맨 앞의 블럭이 누워있는 경우

맨 앞의 블럭이 서있는 경우와 맨 앞의 블럭이 누워있는 경우중 서로 겹치는 경우가 있을까?

절대 없을 것이다. 앞의 블럭 모양이 다르기 때문이다.

그렇기 때문에, N개의 줄에 타일을 배치하는 경우의 수는 맨 앞의 타일 이 서있는 경우 + 맨 앞의 타일 이 누워있는 경우로 바꿔서 생각해볼 수 있다.

N개의 줄에 타일을 배치하는 경우의 수  = 맨 앞의 타일이 서있는 경우 + 맨 앞의 타일 이 누워있는 경우

그렇다면, 두 개의 경우를 하나씩 살펴보자.

맨 앞의 타일 이 서있는 경우라면, 맨 앞의 타일 은 고정이기 때문에 뒤의 N-1줄에 타일을 배치하는 경우의 수가

곧 타일을 배치하는 전체 경우의 수이다.

즉 맨 앞의 타일 이 서있는 경우의 수는 N-1줄에 타일 을 배치하는 경우의 수이다.

N개의 줄에서 맨 앞의 블럭이 서있는 경우의 수  = N-1 줄에 타일을 배치하는 경우의 수

이번엔, 두 번째 경우를 보자.

맨 앞의 타일이 누워있는 경우이다. 타일이 누워있다면 총 두 줄을 점유하기 때문에, 뒤의 N-2줄에 타일을 배치하는 경우가 곧 타일을 배치하는 경우의 수가 된다.

N개의 줄에서 맨 앞의 블럭이 누워있는 경우의 수  = N-2 줄에 타일을 배치하는 경우의 수

이제, 맨 위에서 처음으로 구했던 명제를 보자.

N개의 줄에 타일을 배치하는 경우의 수 

= 맨 앞의 타일이 서있는 경우 + 맨 앞의 타일 이 누워있는 경우

=  N-1 줄에 타일을 배치하는 경우의 수 + N-2 줄에 타일을 배치하는 경우의 수

이런 결론에 도달할 수 있다.

우리는 직접 계산을 통해, N이 1, 2, 3 일 때의 경우의 수는 쉽게 구할 수 있다.

D(N) 이 N개의 줄에 타일을 배치하는 경우의 수라면,

D(1) = 1;

D(2) = 2;

D(3) = 3;

이렇게 될 것이다.

이제부터 반복문을 돌며 값을 구하면 된다.

D(4) = D(3) + D(2)

D(5) = D(4) + D(3)

           .

           .

           .

           .

D(N) = D(N - 1) + D(N - 2) 까지 답을 구하면 문제는 끝난다.

풀이 코드

#include <string>
#include <vector>

using namespace std;

int solution(int n) 
{  
    std::vector<int> DP(n + 1, 0);
    
    DP[1] = 1;
    DP[2] = 2;
    DP[3] = 3;
    
    int CurIndex = 4;
    int EndINdex = n;
    
    while(CurIndex <= n)
    {
        DP[CurIndex] = (DP[CurIndex - 1]  + DP[CurIndex - 2]) % 1000000007;       
        CurIndex++;
    }
    
    return DP[n];
}

풀이는 정말 간단하다.

위에서 구했던 점화식을 그대로 코드로 작성하면 된다.

코드를 짜는게 어렵다기보단, 아이디어를 떠올리는게 다소 어려울 수 있었던 문제이다.

결과

문제의 입력으로 현재 피로도 K와 던전의 정보 숫자 쌍이 주어진다.

던전의 정보, 숫자 쌍 중에 첫 번째 숫자는 입장시 요구되는 최소 피로도를 의미하며 두 번째 숫자는 소모 피로도를 의미한다. 

즉, 입력중 첫 번째 원소인 [[80, 20]] 을 기준으로 본다면 입장하기 위해서 현재 피로도는 최소 80이어야 하며, 입장시 20이 소모된다는 뜻이다.

피로도 조건에 따라 던전을 어떤 순서로 갔을 때 최대 몇 개까지 던전을 클리어할 수 있는가? 를 구하는 문제이다.

문제 풀이

이 문제는 그렇게 복잡한 알고리즘을 요구하는 문제는 아니고, 모든 경우의 수를 하나하나 비교해보는 문제이다.

핵심은 그 경우의 수를 어떻게 구하느냐인데, 여러 방식이 있겠지만 본인은 순열을 사용하였다.

먼저, 던전의 개수만큼의 벡터를 resize하여, 각 원소에 인덱스 저장하였다.

이렇게 저장해놓은 뒤, next_permutation 을 이용해서 모든 경우의 수를 탐색하며 결과를 추적하였다.

순열 배열의 값이 1 - 2 - 3 - 4 인 경우, 1번 던전 -> 2번 던전 -> 3번 던전 -> 4번 던전 순으로 시뮬레이션 하였고

1 - 3 - 2 - 4 인 경우,  1번 던전 -> 3번 던전 -> 2번 던전 -> 4번 던전의 순으로 순열 배열의 원소와 동일하게 시뮬레이션 하였다.

풀이 코드

std::vector<int> Nums(dungeons.size());

for(int i = 0; i < Nums.size(); i++)
{
    Nums[i] = i;
}

먼저, 배열의 값에 인덱스를 넣어주었다.

 int MaxDungeons = 0;
    
while(true)
{
    int NumOfDungeons = 0;
    int CopyK = k;

    for(int i = 0; i < Nums.size(); i++)
    {
        if(CopyK < dungeons[Nums[i]][0])
        {
            break;
        }
        else
        {
            CopyK -= dungeons[Nums[i]][1];
            NumOfDungeons++;
        }
    }

    MaxDungeons = std::max(MaxDungeons, NumOfDungeons);

    if(std::next_permutation(Nums.begin(), Nums.end()) == false)
    {
        break;
    }
}

이후는 위에서 설명한 것과 같다.

현재 피로도가 던전의 입장 피로도보다 낮다면 반복문을 즉시 중지하며,

현재 피로도가 던전의 입장 피로도보다 높거나 같다면 피로도를 소모한 뒤 NumOfDungeons를 증가시켰다.

(NumOfDungeons 는 클리어한 던전의 수이다.)

이후, MaxDungeons를 갱신한 뒤, next_permutation을 이용하여 다음 경우의 수로 배열의 값을 변경하여 주었다.

반복문이 끝난 뒤, MaxDungeons를 반환하면 끝이다.

결과

사실, 순열을 이용해서 모든 경우의 수를 탐색하는 것은 시간복잡도가 상당하다.

하지만, 해당 문제는 던전의 수가 최대 8개로 제한되어 있었기 때문에 이런 방법이 가능한 것이다.

게임 프로그래밍을 배우면서, 처음에 헤메이게 되는 들이 몇 가지 있는데, 그 중 하나가 로컬과 월드의 개념이다.

나중에 보면 정말 간단한 개념인데, 왜 그 땐 참 헷갈렸을까?

로컬 스페이스와 월드 스페이스.

간단하게 정리하면 이렇다.

로컬은 상대적인 것.

월드는 절대적인 것.

(참고로 언리얼 엔진에서도 로컬 트랜스폼은 Relative로 표현한다.)

그렇다면, 로컬은 뭔데 상대적이라는 거고 월드는 뭔대 절대적이라는 걸까?

먼저, 하나의 예시를 들어보겠다.

우주에는 태양이 있고, 태양 주위를 도는 지구가 있다.

실제에선 지구가 타원을 그리며 공전하지만, 이해하기 쉽게 정확히 원을 그리며 공전한다고 가정해보자.

주황색 원이 태양이며, 검은색 원이 지구이다.

태양은 (0,0)좌표에 존재하고 지구는 태양과 중심사이의 거리가 10이라고 해보자.

이 때, 지구는 계속 태양 주위를 돌며 공전하지만, 태양과의 거리는 10으로 항상 일정할 것이다.

만약 지구가 태양의 정확히 오른쪽에 존재한다면 지구의 좌표는 (10, 0) 일 것이다.

정확히 위에 존재한다면, (0, 10) 일 것이고, 정확히 왼쪽이라면 (-10, 0) 일 것이며, 정확히 아래라면 (0, -10) 일 것이다.

그렇다면, 태양이 만약 (30, 30)으로 이동한다면?

지구는 항상 태양을 기준으로 움직이기 때문에, (30, 30) 을 기준으로 10만큼 거리가 떨어진 위치에서 공전을 할 것이다.

이 개념에서 보자. 지구는 항상 태양을 기준으로 10이라는 고정된 수치만큼 떨어진 거리에 위치한다.

태양이 움직이면, 지구의 좌표도 태양이 이동한 만큼 이동할 것이다.

여기서, 10이라는 거리가 로컬 좌표와 동일한 개념이다.

로컬 좌표는 특정 좌표를 기준으로 얼만큼 떨어져 있는가? 를 의미한다.

반면, 지구가 정확히 태양의 왼쪽에 위치한다고 가정했을 때,

태양이 (0,0) 일 때 지구는 (10, 0) 이었지만, 태양이 (30, 30)으로 이동하게 되면 지구는 (40, 0) 으로 이동한다.

여기서 (40, 0)이라는 지구의 좌표가 월드 좌표와 동일한 개념인 것이다.

모든 사물을 동일한 공간에 배치했을 때, 최종적으로 어디에 위치하는가? 이게 월드 좌표의 개념이다.

물론, 이런 로컬 공간, 윌드 공간이 아니라, 로컬 좌표와 월드 좌표에 대한 개념이다.

이 개념은 위치 뿐만이 아니라, 크기와 회전에 대해서도 적용할 수 있다.

로컬 공간은 혼자만 있는 공간에서 지니고 있는 크기, 회전, 이동에 대한 수치이다.

부모 자식 관계가 없다면, 크기는 1을 기준으로, 회전은 (0, 0, 0)을 기준으로, 위치는 (0, 0, 0)을 기준으로 할 것이다.

하지만, 다른 물체와 부모 자식 관계가 맺어진다면, 기준은 부모의 크기, 부모의 회전, 부모의 위치가 된다.

즉, 로컬 공간에 있는 물체의 기준점은 언제 어디서든 바뀔 수 있다.

절대적인 개념이 아닌 것이다.

하지만, 월드 공간에서의 좌표는 무조건 (0,0,0)이 기준이다. 월드 공간의 기준점은 모든 물체가 공유한다.

지구라는 오브젝트가 태양이라는 오브젝트를 부모로 두고 있다면,

월드 공간에는 태양이라는 오브젝트가 배치되고, 그 태양으로부터 10만큼 떨어진 위치에 지구가 배치되는 것이다.

그렇다면 이 개념이 어디에 어떻게 쓰일까?

물론, 여러가지 로직에 사용될 수 있지만 매쉬와 버텍스에 사용되는 것을 예시로 들고 싶다.

이 주전자를 게임 내에서 옮긴다고 해보자. 기본적으로 이런 매쉬들은 버텍스라는 점들의 집합이다.

도형을 보면 여러개의 삼각형으로 이루어져 있는데, 이 삼각형들은 폴리곤이라 하며 삼각형의 각 꼭짓점을 버텍스라고 한다.

만약, 로컬 좌표라는 개념이 없이 월드만을 기준으로 이 주전자를 움직인다고 하면 언뜻 보기에도 수백개는 되어 보이는 버텍스들의 위치관계를 정밀하게 재현하며 이동하려면 참 귀찮고 짜증나는 연산이 요구될 것이다. 이동은 그렇다 치더라도 회전까지 고려하게 되면 정말 복잡한 연산이 필요할 것이다.

하지만, 실제론 어떻게 작동하냐면 저 메쉬엔 피봇이라 하는 기준점이 하나 설정되어 있다.

모든 버텍스는 그 피봇을 기준으로 얼만큼 떨어져 있고, 얼만큼 회전했는지 등에 대한 정보를 담고 있을 뿐이다.

저 주전자를 월드 공간에 배치한다면 실제로 우리가 제어하는 것은 피봇 하나이고, 그 피봇을 기준으로 모든 버텍스가 정해진 거리, 정해진 회전값으로 아주 균일하게 이동하는 것이다.

또 하나의 예시를 들어보자면, 플레이어와 무기의 관계를 보자.

위 게임에서 플레이어를 보면, 플레이어는 무기를 들고 있다.

무기와 플레이어는 한 덩어리가 아니다. 플레이어를 기준으로 어떠한 위치에 존재할 뿐이다.

여기서, 로컬 좌표의 개념 없이 무기의 좌표를 플레이어의 손에 딱 맞추려면 무슨 짓을 해야할까?

플레이어가 이동할 때마다, 애니메이션이 바뀔 때마다 손의 위치를 찾아가며, 무기의 위치를 갱신해야 할 것이다.

하지만 로컬 좌표의 개념을 이용한다면, 무기의 부모를 플레이어의 손으로 설정한 뒤 거리, 회전, 크기 값을 조정해주면 그 이후엔 우리가 신경 쓸 일이 없다.

로컬 좌표와 월드 좌표는 굉장히 간단한 개념이지만, 처음 배울 땐 왠지 모르게 참 헷갈리는 존재이다.

(나만 그랬나??)

누구에게든 도움이 됐으면 좋겠다

STL의 경우 Vector, Set, Map에 해당하는 3가지 자료구조에 대해 알아볼 것이다.

언리얼 엔진에서 std::vector는 TArray, std::set은 TSet, std::map은 TMap이다.

먼저, 시간 복잡도에 알아보자.

신기하게도, 거의 모든 시간복잡도가 O(1)이다.

STL의 경우 Set과 Map의 탐색 시간복잡도는 O(logN) 이다.

어떻게 이럴 수 있는지 간단히 알아보자.

먼저, TArray의 경우는 std::vector와 거의 동일하다.

배열 기반의 자료구조이며, 인덱스로 접근이 가능하다. 메모리에 연속적으로 위치하기 때문에 캐시적중률이 높으며, 삽입과 삭제는 다소 긴 연산을 하게된다.

TSet과 TMap은 STL과 많이 다르다.

차이점을 알아보자.

std::set, std::map

• 포인터, 노드 기반의 자료구조
• 데이터가 삽입, 삭제될 때마다 정렬 진행
• 데이터의 개수만큼 메모리가 할당

TSet, TMap

• 배열, 해시테이블 기반의 자료구조
• 데이터를 정렬하지 않음
• 배열 형태이기 때문에, 데이터의 개수보다 많은 메모리를 할당

먼저, 첫번째 차이점을 알아보자.

std::set과 std::map은 포인터, 노드 기반의 자료구조이다. 그렇기 때문에, 배열 기반의 자료구조보다 낮은 캐시적중률을 보유하고 있다. 동일한 시간복잡도를 가진 연산을 하더라도 배열기반의 자료구조보다 더 느릴 수 밖에 없다.

반면, TSet과 TMap은 그러한 성능 차이를 극복하기 위해, 배열 형태로 구성되어있다. 메모리를 연속적으로 붙임으로써 높은 캐시적중률을 갖게 된다. 

또한, TSet과 TMap은 해시테이블을 기반으로 데이터를 보관하게 된다.

해시테이블이란, 데이터를 암호화하여 빠르게 접근하기 위한 것이다.

예를들어, "ABCDEFG"라는 key를 가진 데이터를 std::set에 넣는다고 한다면, key를 탐색할 때마다 문자열의 길이만큼 반복문을 돌며 검사를 해야한다. 이는 문자열의 길이가 길어질수록 더 많은 연산을 요구할 것이다.

하지만, ABCDEFG 를 1이라는 숫자로 대체할 수 있다면?

길이가 몇이든지 단 1번의 비교연산으로 key를 찾을 수 있다.

이 것이 해시테이블이다. 데이터를 암호화하여 단순한 형태로 만들어 탐색을 쉽게 하는 것이다. TSet과 TMap은 해시테이블 형태로 구성되어, 빠른 key탐색과 접근을 허용한다고 한다.

두 번째 차이점

std::set과 std::map은 데이터가 삽입, 삭제될 때마다 자동 정렬을 하며 재구축을 진행한다. 이로 인해, 오버헤드가 발생할 수 밖에 없는데 TSet과 TMap은 정렬을 진행하지 않는다. (중복 검사는 진행한다.)

정렬을 하지 않기 떄문에, 당연히 삽입, 삭제 연산이 std::map, std::set에 비해 빠를 수 밖에 없다.

만약 정렬을 원한다면, 멤버함수 sort를 사용하면 된다.

세 번째 차이점

이 것은 TSet,TMap의 단점이라고도 할 수 있는데, 얘네는 배열 기반이기 때문에 데이터를 삭제한다고 해서 메모리를 해제하지는 않는다. 즉, 비어있는 메모리로 남아있는 것이다.

TSet, TMap은 TArray와 다르게 중간에서 데이터가 삭제된다고 하더라도 앞으로 땡기거나 하지 않는다. 그냥 비어있는 채로 냅둔다. 이 비어있는 공간을 슬랙이라고 한다.

물론 언리얼 엔진에선 이 슬랙을 제거하는 방법도 제공해주고 있다.

멤버함수 Shrink를 사용하면 된다. 이는 TArray에도 사용할 수 있다.

배열의 뒤쪽에 남아있는 빈 공간을 모두 제거해서 배열과 메모리 크기를 딱 맞춰준다.

하지만, Shrink는 끝에 있는 슬랙만 제거하기 때문에 중간에 비어있는 놈은 해결할 수 없다.

중간에 있는 슬랙까지 해결하고 싶다면 Compact(), CompactStable() 함수를 사용하면 된다.

Compact()는 슬랙을 지우는 과정에서 순서가 보장되지 않는 함수고, CompactStable()은 순서를 보장한 상태로 슬랙을 지우는 함수이다.

이 두 함수로 중간에 있는 슬랙을 해결한 뒤, Shrink함수를 사용하면 완벽하게 데이터의 개수와 메모리의 크기가 일치하게 되어 내부 단편화를 해결할 수 있다.

언리얼 엔진의 자료구조에 대해 알아보았다. 막상 사용해보면 STL과 다른 점이 꽤 많기 때문에 직접 사용해보며 익혀보는게 좋을 것이다.

이전에 3D 게임 모작 프로젝트를 하면서 알게된 지식 중 감마 코렉션이라는 것이 있다.

간단하지만, 굉장히 중요한 역할을 하는 녀석이다.

감마 코렉션이란, 이미지에 들어가는 감마 보정을 제거하거나 추가하는 모든 과정을 통틀어서 일컫는 단어이다.

감마 보정은 그럼 뭔데? 라는 얘기를 하기 전에 베버의 법칙에 대한 얘기를 먼저 해야한다.

베버의 법칙이란, 인간은 자극에 대해서 선형적이지 않게 반응한다는 것이다.

예를 들어보자. 

도서관에서 서로 속삭이며 얘기할 때엔, 소리를 조금만 키워도 모두가 알아차릴 수 있을 것이다.

하지만, 콘서트장에서 들리는 함성소리는 그 변화를 쉽게 탐지할 수 없다.

동일하게 0.1이라는 수치만큼의 소리가 변화했다고 하더라도, 도서관에선 그 변화를 느낄 수 있는 반면

콘서트장에선 느낄 수 없을 것이다.

이 것이 베버의 법칙이다.

인간이 자극의 변화를 탐지하는 것은 처음 자극의 크기에 비례한다고 한다. 처음 자극이 작을수록 그 변화를 쉽게 느낄 수 있는 반면, 처음 자극이 강하다면 그 변화를 쉽게 알아차리지 못한다.

이 것은 시각에서도 마찬가지이다. 우리는 어두운 곳에선 생각보다 쉽게 명암을 구분하지만, 아주 밝은 곳에선 명암을 쉽게 구분하지 못한다고 한다. 

실제로 빛의 세기에 대한 감각반응을 그래프로 그려보면, 밝은 곳보다 어두운 곳에서 민감하게 반응한다고 한다. 

그렇다면, 이게 그래픽스랑 무슨 상관일까?

모니터를 생각해보자.

모니터는 색상을 RGB값으로 출력한다. 0이 가장 어두운 색이라면, 1이 가장 밝은 색일 것이다.

보통 디자이너가 그림을 그릴 때, 현실에서 본 색상, 밝기를 기준으로 그림을 그릴 것이다.

두 물체의 밝기 차이를 현실에서 0.1정도라 느꼈다면, 0.1의 차이로 그림을 그리게 될 것이다.

하지만, 막상 모니터에 출력해보면 상상했던 것과는 다르게 출력될 것이다. 왜냐하면, 우리가 0.1 차이라고 느꼈던 그 차이는 실제 밝기의 차이가 아니라 그렇게 인지했을 뿐이다. 반면, 모니터는 실제 0.1 차이만큼의 밝기로 출력할 것이다.

이 간극을 좁혀서 현실에서 보는 것처럼 자연스럽게 이미지를 출력하기 위해, 모니터는 색상을 출력할 때 의도적으로 어두운 색상을 강조하여 출력하고 있다. 이를 감마 보정이라 한다. 수치는 디스플레이마다 다를 수 있지만, 일반적으로 최종 색상에 2.2f 제곱을 하여 출력한다고 한다.

하지만, 이미지 파일, 사진 등은 다르다고 한다. 카메라는 기본적으로 선형으로 빛을 기록한다.

하지만, 위에서 말했듯이 인간은 어두움에 더 민감하기 때문에 선형으로 기록된 색상은 밝은 부분에 대해 너무 적은 정보를 담고 있고, 어두움에 대해선 너무 많은 정보를 담고있게 된다. 그렇기 때문에, 모니터와는 반대로 1/2.2f를 제곱하여 색상을 더 밝게하여 저장한다고 한다. 

이렇게 하는 것이 파일 저장의 용량면에 있어서도 여러가지로 이득이라고 한다. (감마가 아닌 다른 방식으로 색을 조율하려면, 채널당 8bit가 아니라 16bit가 필요하다네요.)

그래서 이걸 왜 알아야됨??

이건 쉐이더를 쓸 때 중요해진다.

0.5, 0.5, 0.5의 RGB를 가진 이미지를 만들어서 저장했다고 치자.

이 이미지를 쉐이더에서 샘플링하고, 색상 * 2 를 한다고 치면, 우리는 값이 1.0 이 나오기를 기대할 것이다.

하지만, 실제로는 1.0 을 넘는 값이 나온다.

왜?? 이미지는 1/2.2f 제곱을 한 상태로 저장이 되어있기 때문이다.

그렇기 때문에, 쉐이더에선 이런 이미지들을 샘플링한 뒤에 색상에 2.2f 제곱을 하는 과정을 거쳐줘야 제대로 된 연산을 할 수 있게 된다. 

물론, 모든 연산을 마친 후엔 다시 색상에 1.0f/2.2f 제곱을 해주어야 한다.

하지만, 가끔 이러한 연산을 해주지 않아도 되는 것들이 있다.

노말맵, 러프니스 맵 등 색상이나 이미지 정보가 아니라 수치에 관한 정보를 담고 있는 이미지들은 저장할 때 감마보정을 하지 않고, 그대로 RGB를 저장할 수도 있기 때문에 샘플링하고자 하는 이미지가 어떻게 저장되어 있는지 꼼꼼히 확인해보아야 한다. 

참고로 아래의 사진은 비교 사진이다.

(좌 - 감마를 고려한 상태로 쉐이딩, 우 - 감마를 고려하지 않고 쉐이딩)