
주어진 추의 조합으로 측정할 수 없는 무게의 최소값을 구하면 된다.
위에서 주어진 조건의 경우, 아래와 같다.
1 -> 1
2 -> 2
3 -> 3
4 -> 1 + 3
5 -> 2 + 3
.
.
.
.
20 -> 2 + 3 + 7 + 8
21 -> 측정 X
이 때, 21을 출력해주면 답이 된다.
문제 풀이
해당 문제는 아이디어를 구상하기가 다소 어려운 문제라고 생각했다.
본인도 고민을 정말 많이 했다.
먼저, 해당 문제에서 답을 구하려면 주어진 추를 무게순으로 정렬해주어야 한다.
{3, 1, 6, 2, 7, 30, 1} -> {1, 1, 2, 3, 6, 7, 30}
이제, 이 정렬된 추를 기준으로 측정할 수 있는 무게들을 구해야 한다.
기본적인 아이디어는 이렇다.
만약, 무게순으로 정렬된 5개의 추(a, b, c, d, e)가 있다고 해보자.
a, b, c를 사용해서 1, 2, 3, 4, 5 를 모두 측정할 수 있다고 가정했을 때, C의 무게가 5라면, 6~ 10까지 숫자 또한 모두 측정할 수 있다.
왜냐하면, 1 + 5 = 6, 2 + 5 = 7, 3 +5 =8, 4 + 5 = 9, 5 + 5 = 10 이므로, 1~5를 모두 측정할 수 있다면 6~10까지 또한 측정할 수 있는 것이다.
이를 일반화 해보자.
만약 1~(n - 1)번째 추까지 사용해서 1~K 까지의 무게를 모두 측정할 수 있다고 가정해보자.
이 때, n번째 추의 무게가 W라면, n번째 추를 사용한다면 1 + W ~ K + W 또한 측정할 수 있다.
그런데, 1~K와 (1 + W) ~ (K + W)가 만약 겹치지 않는다면?
예를들어 K가 5이고, W가 7이라고 해보자.
1 ~ 5, 8 ~ 12 의 범위가 된다.
즉, 6과 7은 n번째 추를 사용해서 측정할 수가 없는 것이다.
이렇게 범위를 구할 수 있다면, 6과 7중 최소값인 6을 정답이라고 표현할 수 있다.
이번엔, 문제에서 주어진 예제를 보며 이해해보자.

주어진 추를 무게순으로 정렬하면 위의 그림과 같다.
추를 하나도 사용하지 않은 상태에서 측정할 수 있는 무게의 범위는 0 ~ 0이다.
맨 앞의 추를 사용해보자.
맨 앞의 추를 사용하게 되면, 측정할 수 있는 범위는 아래와 같아진다.

두 범위는 하나로 합쳐질 수 있기 때문에, 0~1이라고 표현할 수 있다.

이번엔, 두 번째 추를 사용해보자.

위 그림과 같이 범위를 갱신할 수 있다.
세 번째 추도 사용해보자.

이번엔, 위의 그림과 같이 표현할 수 있다.
이렇게 쭉 가서 6번째 추까지 가보도록 하겠다.
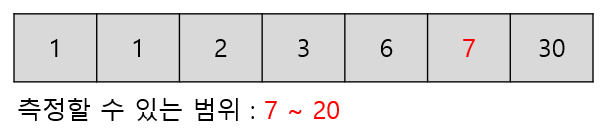
범위를 위 그림과 같이 갱신할 수 있다.
여기서 다음 추를 사용하게 되면 어떻게 될까?

측정할 수 있는 두 범위가 겹치지 않는 구간이 존재한다.
즉, 21~36까지의 숫자는 주어진 추로 측정할 수 없는 것이다.
그러므로 정답은 최소값인 21이 된다.
풀이 코드
int NumOfWeight = 0;
std::cin >> NumOfWeight;
std::vector<int> Weights(NumOfWeight);
for (int i = 0; i < NumOfWeight; i++)
{
std::cin >> Weights[i];
}
std::sort(Weights.begin(), Weights.end());
추의 무게를 모두 입력받고 저장한 뒤, 무게순으로 정렬해주었다.
int LastNum = 0;
int Answer = 0;
for (int i = 0; i < NumOfWeight; i++)
{
int MinNum = Weights[i];
int MaxNum = Weights[i] + LastNum;
if (MinNum - LastNum <= 1)
{
LastNum = MaxNum;
}
else
{
break;
}
}
이후, 반복문을 돌며 범위 체크를 해주었다.
앞의 추까지 사용해서 측정할 수 있는 범위의 최대값을 LastNum에 저장해주었고,
현재 추를 사용하여 측정할 수 있는 범위를 MinNum 과 MaxNum으로 표현하였다.
이 때, 만약 MinNum이 LastNum보다 2이상 크다면, 두 범위 사이에 겹치지 않는 구간이 존재한다고 가정하였고 반복문을 탈출해주었다.
Answer = LastNum + 1;
std::cout << Answer;
return 0;
반복문을 탈출했을 때, LastNum까지는 무게 측정이 가능했다는 얘기이기 때문에 LastNum + 1 을 정답으로 출력해주었다.

코드 전문
#include <iostream>
#include <vector>
#include <algorithm>
void Init()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
}
int main()
{
Init();
int NumOfWeight = 0;
std::cin >> NumOfWeight;
std::vector<int> Weights(NumOfWeight);
for (int i = 0; i < NumOfWeight; i++)
{
std::cin >> Weights[i];
}
std::sort(Weights.begin(), Weights.end());
int LastNum = 0;
int Answer = 0;
for (int i = 0; i < NumOfWeight; i++)
{
int MinNum = Weights[i];
int MaxNum = Weights[i] + LastNum;
if (MinNum - LastNum <= 1)
{
LastNum = MaxNum;
}
else
{
break;
}
}
Answer = LastNum + 1;
std::cout << Answer;
return 0;
}'코딩테스트 문제 풀이 (C++)' 카테고리의 다른 글
| 백준 2493 - 탑 (C++) (0) | 2024.04.26 |
|---|---|
| 백준 12904 - A와 B (C++) (0) | 2024.04.24 |
| 백준 2668 - 숫자 고르기 (C++) (0) | 2024.04.24 |
| 백준 3758 - KCPC (C++) (0) | 2024.04.22 |
| 백준 2170 - 선 긋기 (C++) (0) | 2024.04.21 |