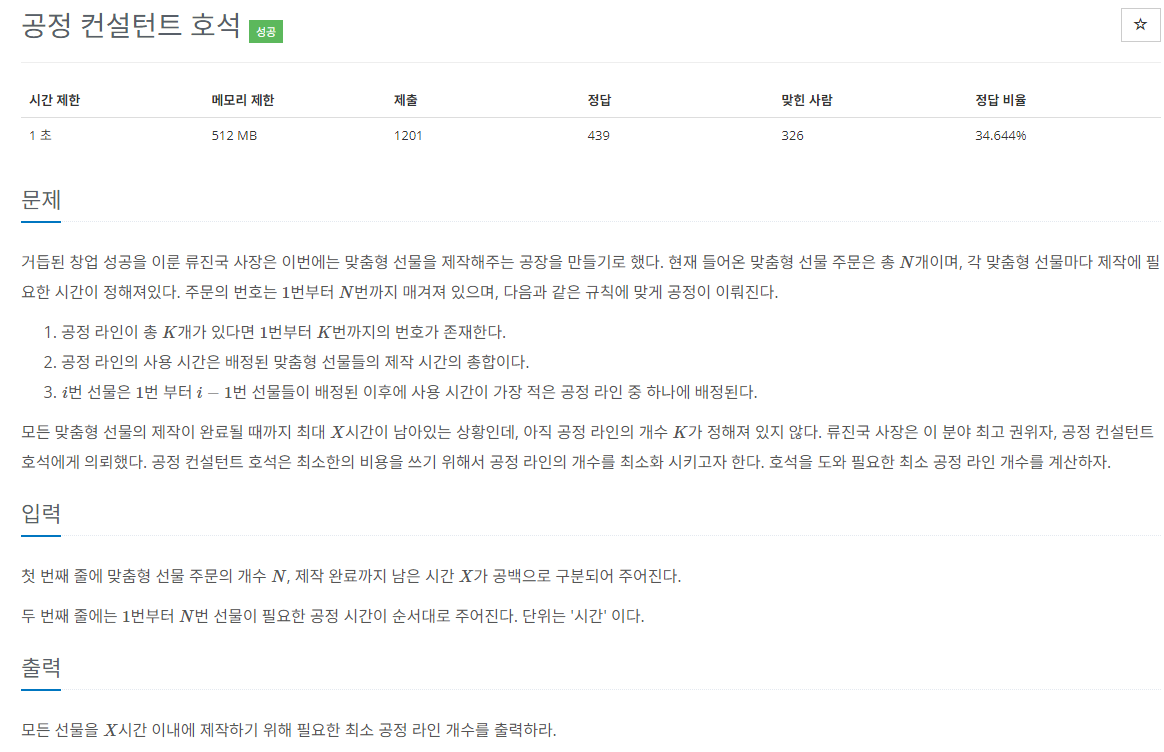
전형적인 이분탐색 문제이다. 다만, 공정의 개수를 K라고 했을 때 소요되는 시간을 구하는 함수를 만드는 것이 중요한데 우선순위 큐를 사용하면 쉽게 만들 수 있다.
공정에서 현재 사용시간이 가장 적은 공정에 물픔을 넣어야 하므로 우선순위 큐가 낮은 숫자가 top으로 오도록 한 뒤에 top의 숫자에 현재 맞춤형 선물의 제작시간을 더해가며 우선순위 큐를 갱신해주면 된다.
이 때, 모든 공정에서 걸리는 시간중 최대 시간이 K개의 공정을 사용할 때 걸리는 시간이므로 최대값도 함께 갱신해야 한다.
이분탐색으로 1~100000 사이에서 최적의 공정 개수를 구하면 된다. (다만, left를 0으로 하면 안된다. 본인은 이거때문에 시간을 좀 날렸다... 공정은 반드시 1개 이상 사용해야 하므로...)
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
void Init()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
}
int GetCostSum(std::vector<int>& _TimeCost, int _Mid)
{
std::priority_queue<int, std::vector<int>, std::greater<>> TimeCostPerProcess;
int MaxTime = 0;
for (int i = 0; i < _TimeCost.size(); i++)
{
if (TimeCostPerProcess.size() < _Mid)
{
TimeCostPerProcess.push(_TimeCost[i]);
MaxTime = std::max(MaxTime, _TimeCost[i]);
}
else
{
int MinTime = TimeCostPerProcess.top();
TimeCostPerProcess.pop();
TimeCostPerProcess.push(MinTime + _TimeCost[i]);
MaxTime = std::max(MaxTime, MinTime + _TimeCost[i]);
}
}
return MaxTime;
}
int main()
{
Init();
int NumGift = 0, RemainingTime = 0;
std::cin >> NumGift >> RemainingTime;
std::vector<int> TimeCost(NumGift);
for (int i = 0; i < NumGift; i++)
{
std::cin >> TimeCost[i];
}
int Left = 1;
int Right = 100000;
int Answer = Right;
while (Left <= Right)
{
int Mid = (Left + Right) / 2;
int CurTime = GetCostSum(TimeCost, Mid);
if (CurTime > RemainingTime)
{
Left = Mid + 1;
}
else
{
Right = Mid - 1;
Answer = std::min(Answer, Mid);
}
}
std::cout << Answer;
return 0;
}'매일매일 코테풀기 (일시 중단!)' 카테고리의 다른 글
| (2024-11-07) 5 문제 : 백준 - 9370 (미확인 도착지) (0) | 2024.11.07 |
|---|---|
| (2024-11-07) 4 문제 : 백준 - 17425 (약수의 합) (0) | 2024.11.07 |
| (2024-11-07) 2 문제 : 백준 - 1600 (말이 되고픈 원숭이) (0) | 2024.11.07 |
| (2024-11-07) 1 문제 : 백준 - 16973 (직사각형 탈출) (0) | 2024.11.07 |
| (2024-11-06) 3 문제 : 백준 - 1956 (운동) (1) | 2024.11.06 |