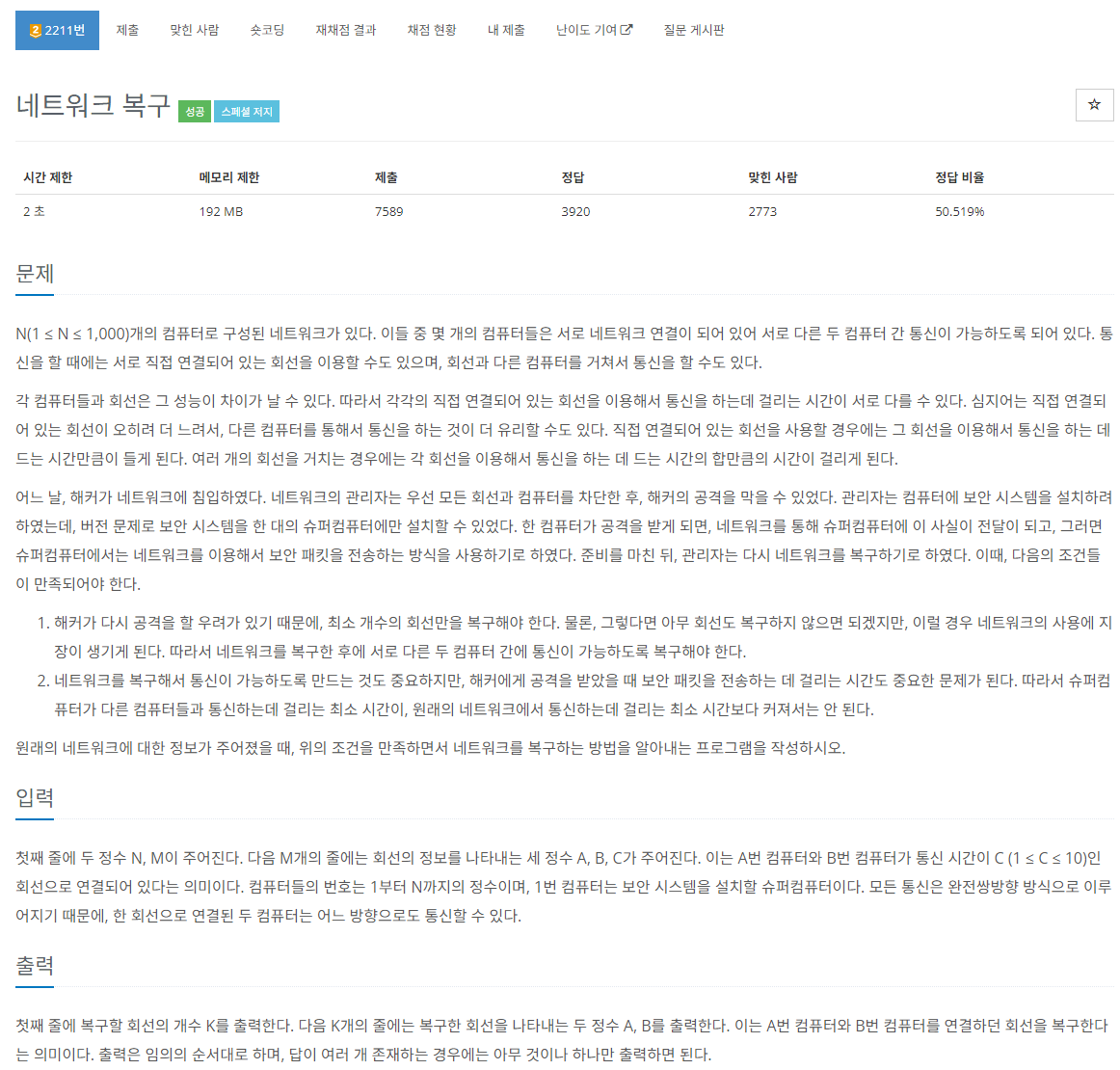
문제가 뭔가 복잡해보이지만, 생각보단 단순한 문제이다. (비문학 문제..)
다익스트라를 통해 최단거리를 갱신하면서 최종적으로 해당 노드에 진입하는 간선을 저장해주면 되는 것이다. 문제는 결국 슈퍼컴퓨터에서 각 컴퓨터로 가는 최단거리를 구하고, 최단 경로에 해당하는 간선을 출력하는 문제이기 때문이다. 최단거리가 갱신될 때 간선도 함께 저장해주면 된다.
무슨말이냐면, 다익스트라를 통해 최단거리를 갱신할 때 2번 노드로 도착하는 간선이 처음엔 1->2번이었다면 2번 노드에 해당하는 간선을 {1, 2}로 저장하고, 나중에 3->2번 간선을 통해 2번 노드의 최단거리가 갱신되었다면 2번 노드에 해당하는 간선을 {3, 2}로 저장하면 된다.
그렇게 노드에 대한 간선을 모두 갱신한 뒤에 모두 출력해주면 된다.
#include <iostream>
#include <vector>
#include <climits>
#include <queue>
#include <map>
void Init()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
}
int main()
{
Init();
int NumComputer = 0, NumLine = 0;
std::cin >> NumComputer >> NumLine;
std::vector<std::vector<std::pair<int, int>>> Link(NumComputer);
for (int i = 0; i < NumLine; i++)
{
int Start = 0, End = 0, Cost = 0;
std::cin >> Start >> End >> Cost;
Link[Start - 1].push_back({ End - 1, Cost });
Link[End - 1].push_back({ Start - 1, Cost });
}
std::vector<int> MinDist(NumComputer, INT_MAX);
MinDist[0] = 0;
std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int>>, std::greater<>> Dijk;
Dijk.push({ 0, 0 });
std::map<int, std::pair<int, int>> Answers;
while (Dijk.size() > 0)
{
auto [CurNode, CurDist] = Dijk.top();
Dijk.pop();
for (int i = 0; i < Link[CurNode].size(); i++)
{
int NextNode = Link[CurNode][i].first;
if (MinDist[NextNode] > CurDist + Link[CurNode][i].second)
{
MinDist[NextNode] = CurDist + Link[CurNode][i].second;
Answers[NextNode] = { CurNode, NextNode };
Dijk.push({ NextNode, MinDist[NextNode] });
}
}
}
std::cout << Answers.size() << "\n";
for (const auto& Pair : Answers)
{
std::cout << Pair.second.first + 1 << " " << Pair.second.second + 1 << "\n";
}
return 0;
}
'매일매일 코테풀기 (일시 중단!)' 카테고리의 다른 글
| (2024-11-06) 1 문제 : 백준 - 1918 (후위 표기식) (0) | 2024.11.06 |
|---|---|
| (2024-11-05) 4 문제 : 백준 - 3108 (로고) (0) | 2024.11.05 |
| (2024-11-05) 2 문제 : 백준 - 2580 (스도쿠) (1) | 2024.11.05 |
| (2024-11-05) 1 문제 : 백준 - 1707 (이분 그래프) (0) | 2024.11.05 |
| (2024-11-04) 3 문제 : 백준 - 12893 (적의 적) (0) | 2024.11.04 |