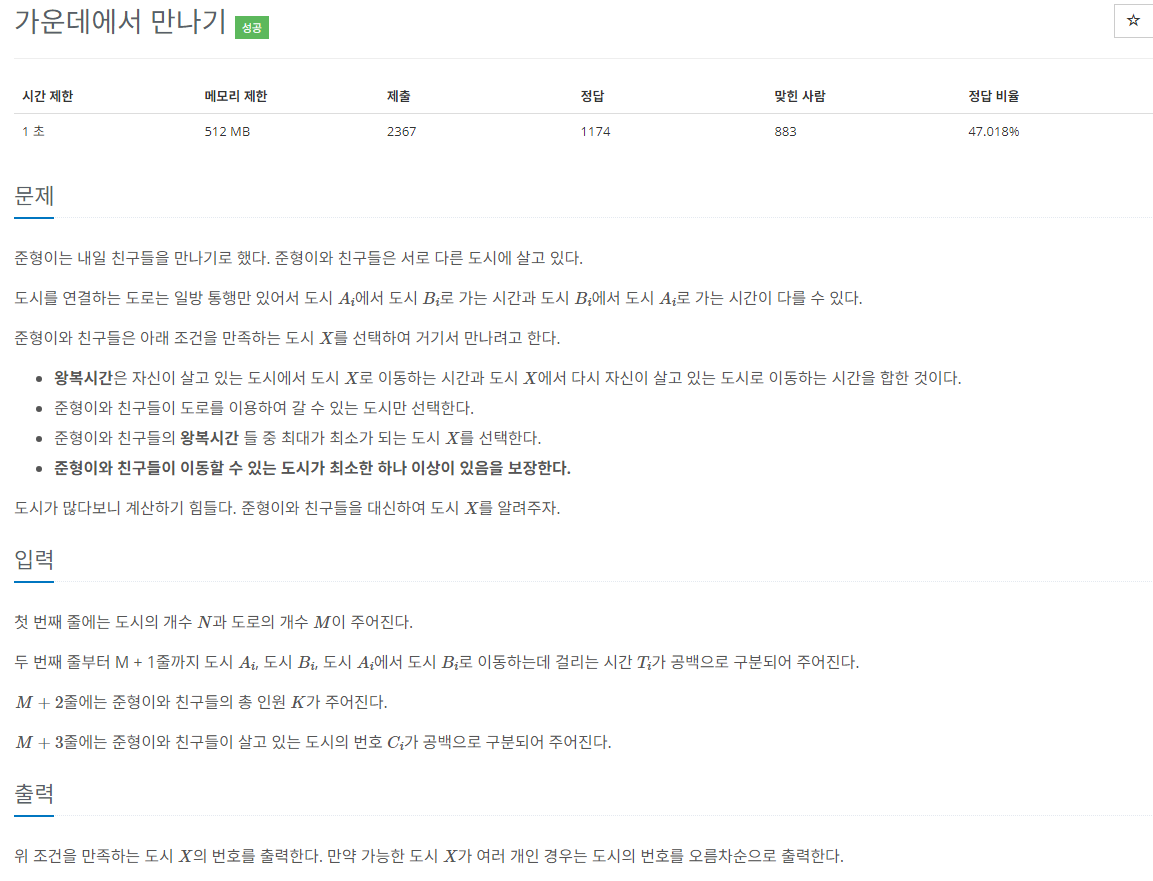
간단한 길찾기 문제이다. 각 친구들이 살고 있는 도시에서 목표 도시로 갔다가 다시 오는 총 비용을 모두 구해야 하기 때문에 플로이드 워셜 알고리즘을 사용하였다.
다익스트라 알고리즘을 사용하면 모든 도시에 대해 왕복 비용을 계산하기 위해 도시의 개수만큼 다익스트라 알고리즘을 수행해야 한다. 도시의 개수가 총 200개로 적어서 그런지 플로이드 워셜 알고리즘이 훨씬 문제 해결 속도가 빨랐다. 본인은 두 방식을 둘 다 해봤는데 다익스트라는 80ms정도 나왔고 플로이드 워셜은 16ms정도가 나왔다.
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <algorithm>
void Init()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
}
int main()
{
Init();
int NumCity = 0, NumRoad = 0;
std::cin >> NumCity >> NumRoad;
std::vector<std::vector<int>> MinCost(NumCity, std::vector<int>(NumCity, INT_MAX / 2));
for (int i = 0; i < NumCity; i++)
{
MinCost[i][i] = 0;
}
std::vector<std::vector<int>> Link(NumCity);
for (int i = 0; i < NumRoad; i++)
{
int Start = 0, End = 0, Cost = 0;
std::cin >> Start >> End >> Cost;
Link[Start - 1].push_back(End - 1);
MinCost[Start - 1][End - 1] = Cost;
}
int NumFriend = 0;
std::cin >> NumFriend;
std::vector<int> LivedCity(NumFriend);
for (int i = 0; i < NumFriend; i++)
{
std::cin >> LivedCity[i];
--LivedCity[i];
}
for (int i = 0; i < NumCity; i++)
{
for (int j = 0; j < NumCity; j++)
{
for (int k = 0; k < NumCity; k++)
{
MinCost[j][k] = std::min(MinCost[j][k], MinCost[j][i] + MinCost[i][k]);
}
}
}
int MinMaxCost = INT_MAX;
std::vector<int> AnswerCities;
AnswerCities.reserve(NumCity);
for (int i = 0; i < NumCity; i++)
{
int MaxCost = 0;
for (int j = 0; j < LivedCity.size(); j++)
{
int StartCity = LivedCity[j];
MaxCost = std::max(MaxCost, MinCost[StartCity][i] + MinCost[i][StartCity]);
}
if (MinMaxCost > MaxCost)
{
AnswerCities.clear();
AnswerCities.push_back(i);
MinMaxCost = MaxCost;
}
else if (MinMaxCost == MaxCost)
{
AnswerCities.push_back(i);
}
}
for (int Answer : AnswerCities)
{
std::cout << Answer + 1 << " ";
}
return 0;
}'매일매일 코테풀기 (일시 중단!)' 카테고리의 다른 글
| (2024-11-01) 1 문제 : 백준 - 1103 (서울 지하철 2호선) (0) | 2024.11.01 |
|---|---|
| (2024-10-31) 5 문제 : 백준 - 1103 (게임) (0) | 2024.10.31 |
| (2024-10-31) 3 문제 : 백준 - 23059 (리그 오브 레게노) (0) | 2024.10.31 |
| (2024-10-31) 2 문제 : 백준 - 2352 (반도체 설계) (0) | 2024.10.31 |
| (2024-10-31) 1 문제 : 백준 - 1818 (책 정리) (0) | 2024.10.31 |