(2024-10-29) 2 문제 : 백준 - 9576 (책 나눠주기)

 

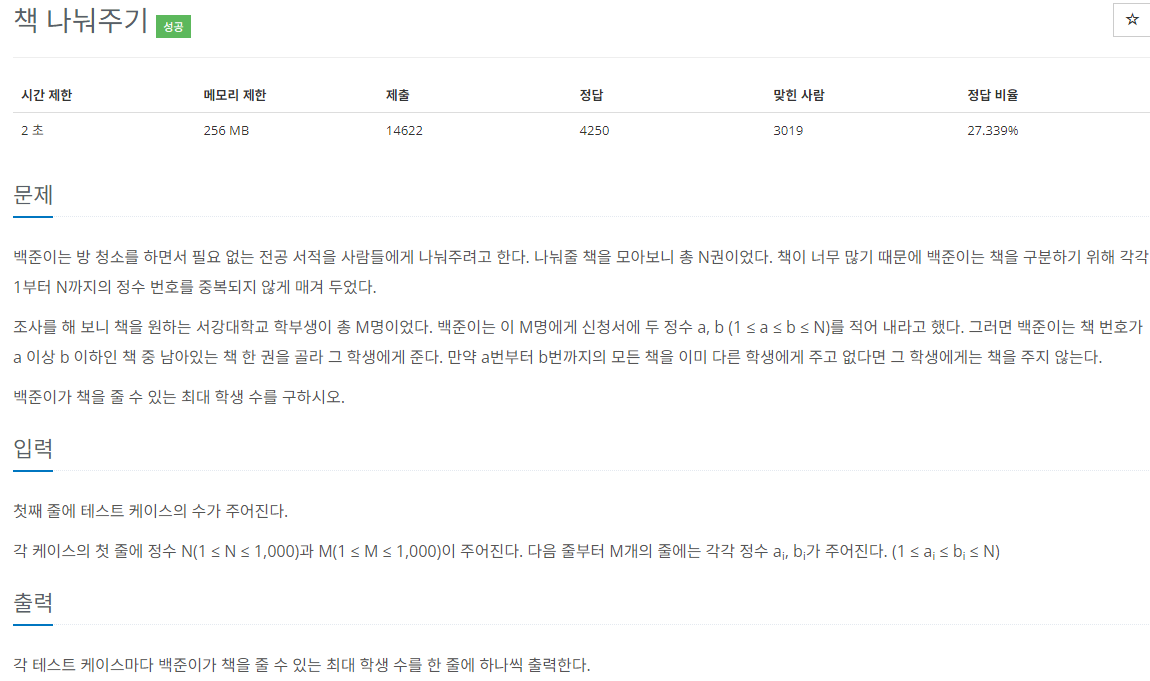
이 문제의 아이디어를 찾는 것을 조금 헤맸는데, 본인은 이분매칭을 활용하였다. 이분 매칭이란, N개의 원소가 속한 그룹 A와 M개의 원소가 속한 그룹 B의 원소들을 1:1로 매칭시킬 수 있는 최대의 수를 구하는 알고리즘이다. 

 

이분 매칭을 활용해서, 조건에 맞도록 사람과 책을 매칭해주면 된다. 이분 매칭은 인접한 노드가 필요한데, 본인은 인접한 노드를 원하는 책의 범위(1~5면 1, 2, 3, 4, 5)로 설정하여 알고리즘을 수행하였다.

 

그런데, 속도가 조금 느렸다. 굉장히 빠르게 푼 다른 사람의 코드를 보았는데 이 사람은 정렬을 활용하였다.

원하는 책의 범위를 (x, y)라고 한다면 (x, y) 페어를 자료구조에 모두 넣어 정렬한 뒤, x가 같은 그룹만 추출하였고, 해당 그룹의 반복문을 돌며 (x~y) 순서대로 책을 분배하였다.

 

본인은 어느 순간부터 어떤 알고리즘을 사용해야 하는지만 고민하게 되었는데, 이런 창의적인 풀이도 떠올릴 줄 아는 여유가 필요할 듯 하다.

 

#include <iostream>
#include <vector>

void Init()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
}

bool Match(const std::vector<std::vector<int>>& _Link, std::vector<int>& _MatchedMan, std::vector<bool>& _IsVisit, int _CurIndex)
{
    _IsVisit[_CurIndex] = true;

    for (int i = 0; i < _Link[_CurIndex].size(); i++)
    {
        int LinkNode = _Link[_CurIndex][i];

        if (_MatchedMan[LinkNode] == -1 || (_IsVisit[_MatchedMan[LinkNode]] == false && Match(_Link, _MatchedMan, _IsVisit, _MatchedMan[LinkNode])))
        {
            _MatchedMan[LinkNode] = _CurIndex;
            return true;
        }
    }

    return false;
}

int main()
{
    Init();

    int NumCase = 0;
    std::cin >> NumCase;

    std::vector<int> Answers(NumCase);

    for (int Case = 0; Case < NumCase; Case++)
    {
        int NumBook = 0, NumMan = 0;
        std::cin >> NumBook >> NumMan;

        std::vector<std::vector<int>> Link(NumMan);
        
        for (int i = 0; i < NumMan; i++)
        {
            int Start = 0, End = 0;
            std::cin >> Start >> End;


            for (int j = Start; j <= End; j++)
            {
                Link[i].push_back(j - 1);
            }
        }

        std::vector<int> MatchedMan(NumBook, -1);
        std::vector<bool> isVisit(NumMan, false);

        int Answer = 0; 

        for (int i = 0; i < NumMan; i++)
        {
            std::fill(isVisit.begin(), isVisit.end(), false);

            if (Match(Link, MatchedMan, isVisit, i) == true)
            {
                Answer++;
            }
        }

        std::cout << Answer << "\n";
    } 

    return 0;
}