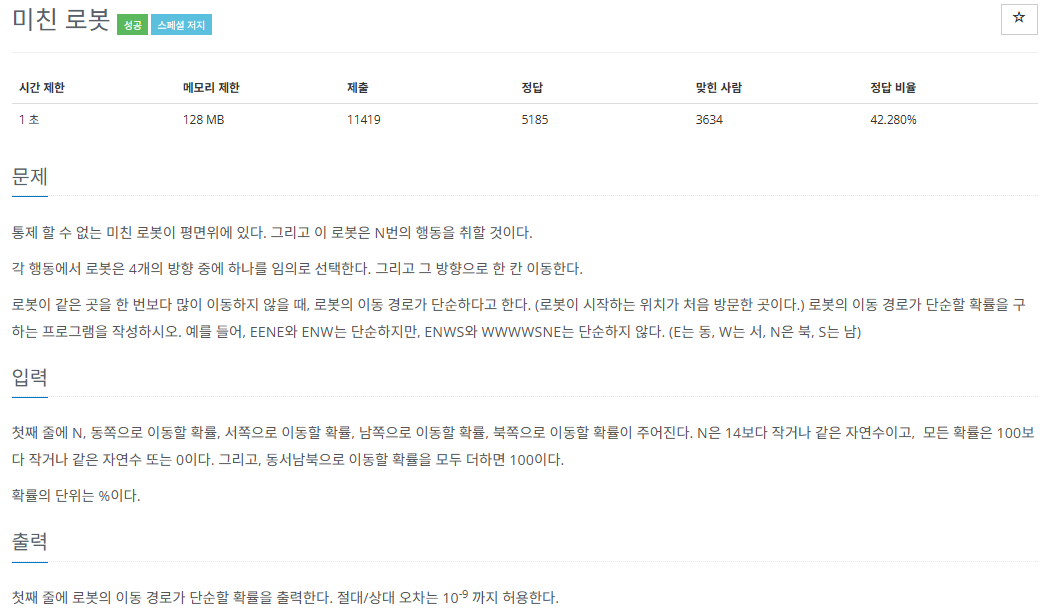
백준 1405 - 미친 로봇 (C++)
로봇이 같은 곳을 한 번보다 많이 이동하지 않는다는 의미가 다소 헷갈렸는데, 방문했던 곳을 다시 방문하지 않는다는 의미였다. 즉, 로봇이 한 번 방문했던 곳을 방문하지 않고 이동하는 경우가 이동경로가 단순한 것이다.
로봇이 동, 서, 남, 북으로 이동할 수 있는 확률이 주어질 때 단순하게 이동하는 경우의 확률을 출력하는 문제이다.
문제 풀이
풀이는 간단하다. 단순하게 이동하는 모든 경우의 수에 대해 확률을 구한 뒤, 그 확률을 모두 더한 값이 정답이 된다.
모든 경우의 수를 어떻게 구할까?
DFS를 사용하면 쉽게 구할 수 있다. 먼저, 로봇이 방문한 거리를 체크하기 위한 이차원 배열을 하나 만들어줄 것이다.
이차원 배열의 크기를 설정할 때, 최소의 크기는 (N * 2 + 1) * (N * 2 + 1) 이 되어야 한다.
배열의 중앙에서 로봇이 이동을 시작한다고 했을 때, 상하좌우 중 한쪽으로만 쭉 이동한 경우 배열의 범위를 초과하지 않으려면 배열의 중앙을 기준으로 양 끝까지 최소 N의 거리가 필요하기 때문이다.
(왼쪽 N + 중앙 1칸 + 오른쪽 N) -> (2 * N + 1)
본인은 N에 따라 가변적으로 변하도록 구현하지는 않았고, 편하게 30 * 30의 배열을 선언하여 사용하였다.
(메모리를 최적화 하고 싶다면 (N * 2 + 1) * (N * 2 + 1) 의 크기로 만드는 것이 당연히 유리하다.)
로봇이 배열의 중앙에서 출발하도록 한 뒤, DFS를 사용하여 이동할 수 있는 모든 경로를 탐색하면 된다.
N번 이동을 마친 뒤, 해당 경로의 확률을 계산한 뒤 그 값을 하나의 변수에 누적해서 더해주면 된다.
풀이 코드
int MoveCount = 0;
double ProbSum = 0;
std::vector<double> Probs;
std::vector<std::vector<bool>> isVisit;
std::vector<int> DirX = { 1, -1, 0, 0 };
std::vector<int> DirY = { 0, 0, 1, -1 };먼저, 위와 같이 전역변수를 선언하였다.
MoveCount는 N을 저장할 변수이며, ProbSum은 출력할 정답을 저장할 곳이다.
Probs는 상하좌우로 이동할 확률을 저장하고 있으며, isVisit는 위에서 설명했던 방문체크 배열이다.
DirX, DirY는 DFS에서 사용되는 상하좌우 이동에 사용될 배열이다.
Probs.resize(4);
std::cin >> MoveCount;
for (int i = 0; i < 4; i++)
{
std::cin >> Probs[i];
Probs[i] /= 100.0l;
}위와 같이 입력을 받아준 뒤, Probs[i]의 모든 원소를 100.0l로 나누어준다.
(25로 입력이 들어오면, 0.25로 변환하여 확률 계산을 편하게 하기 위해서)
isVisit.resize(30, std::vector<bool>(30, 0));위에서 설명했던 것과 같이 방문 배열을 30 * 30으로 resize해주었다.
DFS(15, 15, 0, 1.0l);다음은 DFS 함수를 호출하였다. 첫번째와 두번째 인자는 시작 위치이며, 세번째 인자는 움직인 횟수이다.
4번째 인자는 누적확률이다.
함수 내부 코드를 보자.
void DFS(int _X, int _Y, int _CurMoveCount, double _ProbSum)
{
if (_CurMoveCount >= MoveCount)
{
ProbSum += _ProbSum;
return;
}
isVisit[_Y][_X] = true;
for (int i = 0; i < 4; i++)
{
int NextX = _X + DirX[i];
int NextY = _Y + DirY[i];
if (Probs[i] == 0)
{
continue;
}
if (isVisit[NextY][NextX] == false)
{
DFS(NextX, NextY, _CurMoveCount + 1, _ProbSum * Probs[i]);
}
}
isVisit[_Y][_X] = false;
}가장 위의 조건문을 보면, 이동 횟수가 최대 이동 횟수보다 같거나 크게 된 경우 확률을 ProbSum에 누적해준 뒤 return해주었다.
그 다음, isVisit에 현재 위치에 대한 방문 체크를 해주었다.
다음은 4방향에 대해 아직 방문하지 않은 곳이라면 이동하도록 하도록 하였다.
이동할 때, 현재 방향에 대한 확률을 _ProbSum에 곱하여 확률을 갱신하도록 하였다.
(Probs 배열의 인덱스에 대해 0, 1, 2, 3을 동, 서, 남, 북으로 설정하였다.)
printf("%.10lf", ProbSum);
return 0;DFS가 모두 끝난 뒤, 정답을 출력해주었다.
(문제의 조건이 최대 10^(-9)까지 오차를 인정하고 있기 때문에 소수점 10자리까지 줄력하도록 하였다.)

코드 전문
#include <iostream>
#include <vector>
void Init()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
}
int MoveCount = 0;
double ProbSum = 0;
std::vector<double> Probs;
std::vector<std::vector<bool>> isVisit;
std::vector<int> DirX = { 1, -1, 0, 0 };
std::vector<int> DirY = { 0, 0, 1, -1 };
void DFS(int _X, int _Y, int _CurMoveCount, double _ProbSum)
{
if (_CurMoveCount >= MoveCount)
{
ProbSum += _ProbSum;
return;
}
isVisit[_Y][_X] = true;
for (int i = 0; i < 4; i++)
{
int NextX = _X + DirX[i];
int NextY = _Y + DirY[i];
if (Probs[i] == 0)
{
continue;
}
if (isVisit[NextY][NextX] == false)
{
DFS(NextX, NextY, _CurMoveCount + 1, _ProbSum * Probs[i]);
}
}
isVisit[_Y][_X] = false;
}
int main()
{
Init();
Probs.resize(4);
std::cin >> MoveCount;
for (int i = 0; i < 4; i++)
{
std::cin >> Probs[i];
Probs[i] /= 100.0l;
}
isVisit.resize(30, std::vector<bool>(30, 0));
DFS(15, 15, 0, 1.0l);
printf("%.10lf", ProbSum);
return 0;
}